设有三张不同平面的方程 , ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
设有三张不同平面的方程 ,  ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
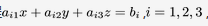 ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为

参考解析
解析:

相关考题:
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3,且η1,η2,η3是3个不同的解向量,则通解是( ).A.x=k1(η-η2)+η3B.x=k1η1+k2η2+η3C.x=k1η1+k2η2+k3η3D.x=k1(η+η2)+η3
单选题“大集中”征管系统中关于现金、待解和直解三张记录缴款数据表的缴款序号说法完全正确的是()。A缴款序号字段都是这三张缴款表的主键B缴款序号在三张缴款表中各有特点,之间不会存在重复的值C缴款序号在三张缴款表之间存在重复的值D这三张缴款表依靠缴款序号字段相互关联
单选题求解线性方程组的追赶法,要求其系数矩阵为( )。A三对角矩阵B上三角矩阵C对称正定矩阵D各类大型稀疏矩阵