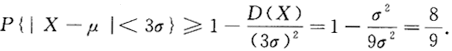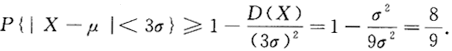设随机变量X的数学期望EX = 1,且满足P{|X-1|>=2}=1/16,根据切比雪夫不等式,X的方差必满足() A.DX>=1/4B.DX>=1/2C.DX>=1/16D.DX>=1
设X服从λ=2的泊松分布,则x的数学期望和方差分别是多少?
设随机变量x的分布函数为则数学期望E(X)等于( )。
设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( ) A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差B.X1,X2,…,Xn,…同分布且有相同的数学期望C.X1,X2,…,Xn,…为同分布的离散型随机变量D.X1,X2,…,Xn,…为同分布的连续型随机变量
设离散型随机变量X的概率分布为求X的数学期望EX及方差DX.
设离散型随机变量x的分布列为①求常数a的值;②求X的数学期望E(X).
设随机变量X1,X2,…,Xn相互独立且在[0,na]上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.
设随机变量X,Y不相关,X~U(-3,3),Y的密度为根据切比雪夫不等式,有P{|X-Y|
设随机变量X方差为2,则根据切比雪夫不等式有估计P{|X-E(X)|≥2}≤_______.
(1)将一均匀的骰子连续扔六次,所出现的点数之和为X,用切比雪夫不等式估计P(14 (2)设随机变量X1,X2,…,X10相互独立且Xi~π(i)(i=1,2,…,10),,根据切比雪夫不等式,P{4
设随机变量X的方差为2,则根据切比雪夫不等式估计P{|X-EX|≥2}≤________.
若随机变量x1,x2,…,xn相互独立同分布于N{μ,2^2},则根据切比雪夫不等式得P{|x-μ|≥2)≤_______.
设X,Y为随机变量,且E(X)=1,E(Y)=2,D(X)=4,D(Y)=9,,用切比雪夫不等式估计P{|X+Y-3|≥10}.
设随机变量x的概率密度为F(x)为X的分布函数,EX为X的数学期望,则P{F(X)>EX-1}=________.
随机变量X的数学期望E(X)=2,方差D(X)=4,则E(X2)=()
设X和Y相互独立,E(X)=1,D(X)=1,E(Y)=1,D(Y)=2,则由切比雪夫不等式得P(|X-Y|≥6)≤()A、1/4B、1/6C、1/12D、1/36
设随机变量X的数学期望E(X)=75,D(X)=5,且P{|X-75|≥k}≤0.05,则k≥()。
设总体X的一个样本如下:1.70,1.75,1.70,1.65,1.75则该样本的数学期望E(X)和方差D(X)的矩估计值分别为()、()
设随机变量X服从二项分布B(10,p),若X的方差是5/2,则p=()
设随机变量X和Y的数学期望都是2,方差分别为1和4,而相关系数为0.5,则根据切比雪夫不等式P{|X-Y|≥6}≤()。
已知E(X)=0,D(X)=3,则由切比雪夫不等式得P{|X|≥6}≤()A、1/4B、1/12C、1/16D、1/36
设X为随机变量,E(X)=0,D(X)=0.5,则由切比雪夫不等式得P{|X|≥1}≤()
设随机变量X和Y的数学期望分别为-2和2,方差分别为1和4,而相关系数为-0.5,则根据切比雪夫不等式P{|X+Y|≥6}≤()。
设随机变量X的方差为2,则P{|X-E(X)|≥2}≤()。
问答题将一枚均匀骰子掷10次,X表示点数6出现的次数,用切比雪夫不等式可估计P{|X-E(X)|
问答题若E(X)=μ,D(X)=σ20,由切比雪夫不等式可估计P{P-3σ〈Xμ+3σ≥_____。
问答题已知E(X)=μ,D(X)=2.5,由切比雪夫不等式可估计P{|X-μ|≥5}≤____.