设为n阶方阵A的两个互不相等的特征值,与之对应的特征向量分别为X1,X2,证明X1,X2不是矩阵A的特征向量。
设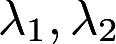
为n阶方阵A的两个互不相等的特征值,与之对应的特征向量分别为X1,X2,证明X1,X2不是矩阵A的特征向量。
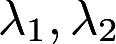为n阶方阵A的两个互不相等的特征值,与之对应的特征向量分别为X1,X2,证明X1,X2不是矩阵A的特征向量。参考解析
解析：
相关考题：
已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。 A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)
两样本均数(X1,X2)作t检验时的无效假设为( ) A、X1，X2分别来自两个不同的总体B、X1，X2分别来自μ1+μ2的总体C、X1，X2分别来自μ1-μ2≠0的总体D、X1，X2分别来自μ1=μ2的总体E、A、B、C、D都不对
设数据x1，x2的绝对误差限分别为0.05和0.005，那么两数的乘积x1x2的绝对误差限E(x1x2)=A、0.005|X2|+0.005|X1|B、0.05|X2|+0.005|X1|C、0.05|X1|+0.005|X2|D、0.005|X1|+0.005|X2|
已知样本x1,x2,…,xn，其中μ未知。下列表达式中，不是统计量的是（）。A. X1 +X2 B. max(x1,x2,…,xn)C. X1 +X2 -2μ D. (X1 -μ)/σE. X1 +μ
设X1,X2,…Xn是简单随机样本，则有（ ）。A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布E.X1与Xn的均值相等
设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。A、α是矩阵-2A的属于特征值-2λ的特征向量B、α是矩阵的属于特征值的特征向量C、α是矩阵A*的属于特征值的特征向量D、α是矩阵AT的属于特征值λ的特征向量
已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。A、β是A的属于特征值0的特征向量B、α是A的属于特征值0的特征向量C、β是A的属于特征值3的特征向量D、α是A的属于特征值3的特征向量
单选题设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。Aα是矩阵-2A的属于特征值-2λ的特征向量Bα是矩阵的属于特征值的特征向量Cα是矩阵A*的属于特征值的特征向量Dα是矩阵AT的属于特征值λ的特征向量
单选题已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。Aβ是A的属于特征值0的特征向量Bα是A的属于特征值0的特征向量Cβ是A的属于特征值3的特征向量Dα是A的属于特征值3的特征向量
问答题设有三个非零的n阶（n≥3）方阵A1、A2、A3，满足Ai2＝Ai（i＝1，2，3），且AiAj＝0（i≠j，i、j＝1，2，3），证明： （1）Ai（i＝1，2，3）的特征值有且仅有0和1； （2）Ai的对应于特征值1的特征向量是Aj的对应于特征值0的特征向量（i≠j）； （3）若α(→)1、α(→)2、α(→)3分别为A1、A2、A3的对应于特征值1的特征向量，则向量组α(→)1、α(→)2、α(→)3线性无关。