设A为三阶方阵,为三维线性无关列向量组,且有求 (I)求A的全部特征值(II)A是否可以对角化?
设A为三阶方阵,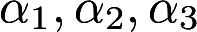 为三维线性无关列向量组,且有
为三维线性无关列向量组,且有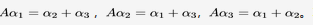 求 (I)求A的全部特征值(II)A是否可以对角化?
求 (I)求A的全部特征值(II)A是否可以对角化?
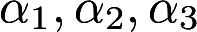 为三维线性无关列向量组,且有
为三维线性无关列向量组,且有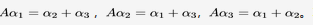 求 (I)求A的全部特征值(II)A是否可以对角化?
求 (I)求A的全部特征值(II)A是否可以对角化?参考解析
解析:

相关考题:
设A为m×n阶矩阵,则齐次线性方程组AX=0只有零解的充分必要条件是(64)。A.A的列向量组线性无关B.A的列向量组线性相关C.A的行向量组线性无关D.A的行向量组线性相关A.A的列向量组线性无关B.A的列向量组线性相关C.A的行向量组线性无关D.A的行向量组线性相关
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆B.矩阵A的迹为零C.特征值-1,1对应的特征向量正交D.方程组AX=0的基础解系含有一个线性无关的解向量
设向量组I:α1α2αr…,可由向量组Ⅱβ1,β2,…βs:线性表示,下列命题正确的是( )。A.若向量组I线性无关.则r≤SB.若向量组I线性相关,则r>sC.若向量组Ⅱ线性无关,则r≤sD.若向量组Ⅱ线性相关,则r>s
设A为4X5矩阵,且A的行向量组线性无关,则( ).《》( )A.A的列向量组线性无关B.方程组AX=b有无穷多解C.方程组AX=b的增广矩阵的任意四个列向量构成的向量组线性无关D.A的任意4个列向量构成的向量组线性无关
单选题设n维列向量组α1,α2,…,αm(m<n)线性无关,则n维列向量组β1,β2,…,βm线性无关的充分必要条件是( ).A向量组α1,α2,…,αm可以由β1,β2,…,βm线性表示B向量组β1,β2,…,βm可以由α1,α2,…,αm线性表示C向量组α1,…,αm与向量组β1,…,βm等价D矩阵A=(α1,…,αm)与矩阵B=(β1,…,βm)β)m
单选题设A为4×5矩阵,且A的行向量组线性无关,则( )。AA的列向量组线性无关B方程组AX(→)=b(→)有无穷多解C方程组AX(→)=b(→)的增广矩阵A(_)的任意四个列向量构成的向量组线性无关DA的任意4个列向量构成的向量组线性无关
单选题n元线性方程组AX(→)=b(→)有唯一解的充要条件为( )。AA为方阵且|A|≠0B导出组AX(→)=0(→)仅有零解C秩(A)=nD系数矩阵A的列向量组线性无关,且常数向量b(→)与A的列向量组线性相关