设U,～N（μ,1）,V～χ^2(n),且U,V相互独立,则T=服从_______分布.
设U,～N（μ,1）,V～χ^2(n),且U,V相互独立,则T=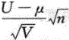
服从_______分布.
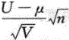服从_______分布.参考解析
解析：由U～N（μ，1），得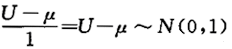
，又U，V相互独立，则.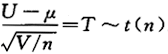
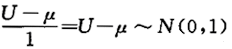，又U，V相互独立，则.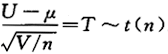
相关考题：
设随机变量X与Y服从正态分布,X~N(u,42),Y~N(u,52),记P1=P{X=u＋5},则() A.对任意数u，都有P1=P2B.对任意实数u，都有P1>P2C.对任意实数u，都有P1D.只有u的个别值才有P1=P2
设有如下关系：则与关系代数表达式π1,4(RS)等价的元组演算表达式为：{t|uv(R(u)∧S(v)∧(33))}；关系代数表达式R÷S的结果集为(34)。A．u[2]=v[1]∧t[1]=u[1]∧t[2]=v[2]B．u[2]=v[1]∧t[1]=u[1]∧t[2]=v[1]C．u[1]=v[1]∧t[1]=u[1]∧t[2]=v[2]D．u[1]=v[1]∧t[1]=u[1]∧t[2]=v[1]
设有如下关系：关系代数表达式R÷S的结果集为(17)。A．u[2]=v[1]t[1]=u[1]t[2]=v[2]B．u[2]=v[1]t[1]=u[1]t[2]=v[1]C．u[1]=v[1]t[1]=u[1]t[2]=V[2]D．u[1]=v[1]t[1]=u[1]t[2]=V[1]
设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布
设随机变量X,y独立同分布,且X～N（0,σ^2）,再设U=aX+by,V=aX-bY,其中a,b为不相等的常数.求： (1)E(U),E(V),D(U),D(V),; (2)设U,V不相关,求常数A,B之间的关系.
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3. 设随机变量U=max{X,Y},V=min{X,Y}. (1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布； (3)判断U,V是否相互独立？(4)求P（U=V）.
单选题考虑离散的盈余过程U（n）=0.5+1.5n－S（n），S（n）=W1+W2+…+Wn为时间段[0，n]内的总索赔额，Wi（i≥1）相互独立共同分布为：则P[U（1）＜0]+P[U（2）＜0]=（ ）。A0.21B0.22 C0.23 D0.24 E0.25
问答题设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。