利用逆矩阵，解线性方程组

利用逆矩阵，解线性方程组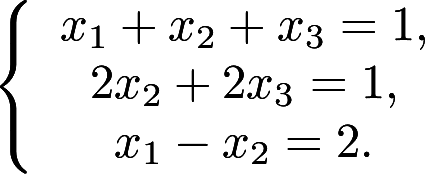

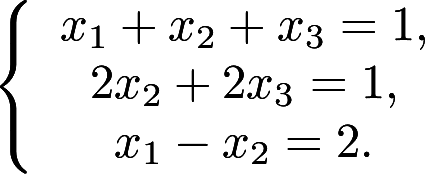
参考解析

解析：

相关考题：

若A是____,则A必为方阵。 A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵
查看答案
没A是n*n常数矩阵(n1),X是由未知数X1,X2,…,Xn组成的列向量,B是由常数b1,b2,…,bn组成的列向量,线性方程组AX=B有唯一解的充分必要条件不是()。 A.A的秩等于nB.A的秩不等于0C.A的行列式值不等于0D.A存在逆矩阵
查看答案
如果线性方程组的系数矩阵满秩,则该方程组一定有解组,且解是唯一的。() 此题为判断题(对，错)。
查看答案
如果线性方程组的系数矩阵满秩则该方程组一定有解且解是唯一的。() 此题为判断题(对，错)。
查看答案
矩阵A是m×n矩阵,齐次线性方程组AX=0只有零解的充要条件是A的列向量线性无关。() 此题为判断题(对，错)。
查看答案
设A是4×6矩阵，r（A）=2，则齐次线性方程组Ax=0的基础解系中所含向量的个数是（ ）A.1 B.2C.3 D.4
查看答案
用迭代法解线性方程组时，迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关，与常数项无关。()
查看答案
什么是线性方程组的系数矩阵和增广矩阵?
查看答案
非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()
查看答案
阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。 用初等变换的方法求解上述线性方程组。
查看答案
用高斯顺序消去法解线性方程组，消元能进行到底的充分必要条件是线性方程组的系数矩阵的各阶顺序主子式均不为0()
查看答案
设A为矩阵，都是线性方程组Ax=0的解，则矩阵A为：
查看答案
若A是m×n矩阵，且m≠n，则当R（A）=n时，齐次线性方程组AX=0只有零解
查看答案
设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。A.若Ax=0仅有零解，则Ax=b有惟一解B.若Ax=0有非零解，则Ax=b有无穷多个解C.若Ax=b有无穷多个解，则Ax=0仅有零解D.若Ax=b有无穷多个解，则Ax=0有非零解
查看答案
设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系A.不存在.B.仅含一个非零解向量.C.含有两个线性无关的解向量.D.含有三个线性无关的解向量.
查看答案
都是线性方程组Ax=0的解，则矩阵A为:
查看答案
解线性方程组其中 .
查看答案
设3阶实对称矩阵A的各行元素之和都为3,向量都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
查看答案
解齐次线性方程组：
查看答案
解非齐次线性方程组
查看答案
利用矩阵的初等变换，求方阵的逆
查看答案
利用逆矩阵解矩阵方程 。
查看答案
利用逆阵解线性方程组:
查看答案
设A为矩阵，都是齐次线性方程组Ax=0的解，则矩阵A为( )。
查看答案
设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。A、无解B、只有零解C、有非零解D、不一定
查看答案
单选题设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。A无解B只有零解C有非零解D不一定
查看答案
单选题n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX(→)＝0(→)有两个线性无关的解，则（　　）。AA*X(→)＝0(→)的解均是AX(→)＝0(→)的解BAX(→)＝0(→)的解均是A*X(→)＝0(→)的解CAX(→)＝0(→)与A*X(→)＝0(→)无非零公共解DAX(→)＝0(→)与A*X(→)＝0(→)仅有2个非零公共解
查看答案
热门标签