证明的充分必要条件是存在非零列向量a及非零行向量使.
证明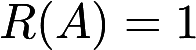
的充分必要条件是存在非零列向量a及非零行向量
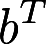使.
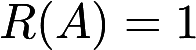的充分必要条件是存在非零列向量a及非零行向量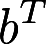使.参考解析
解析：
相关考题：
设A为m×n阶矩阵，则齐次线性方程组AX=0只有零解的充分必要条件是(64)。A．A的列向量组线性无关B．A的列向量组线性相关C．A的行向量组线性无关D．A的行向量组线性相关A.A的列向量组线性无关B.A的列向量组线性相关C.A的行向量组线性无关D.A的行向量组线性相关
设A，B为满足AB=0的任意两个非零矩阵，则必有(56)。A．A的列向量组线性相关，B的行向量组线性相关B．A的列向量组线性相关，B的列向量组线性相关C．A的行向量组线性相关，B的行向量组线性相关D．A的列向量组线性相关，B的列向量组线性相关
设α1，α2，α3均为三维向量，则对任意常数k,l，向量组α1+kα3，α2+lα3线性无关是向量组α1，α2,α3线性无关的 A.A必要非充分条件B.充分非必要条件C.充分必要条件D.既非充分也非必要条件
设a，b均为向量，下列命题中错误的是（）．A、a∥b的充分必要条件是存在实数λ，使b=λaB、a∥b的充分必要条件是a×b=0C、a⊥b的充分必要条件是a·b=0D、D.a⊥b的充分必要条件是（a+·（a-B.=
单选题设向量组Ⅰ：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组Ⅱ：α(→)1，α(→)2，…， α(→)m，β(→)，其秩为s，则r＝s是向量组Ⅰ与向量组Ⅱ等价的（ ）。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件
单选题A是n阶方阵，其秩r＜n，则在A的n个行向量中（ ）.A必有r个行向量线性无关B任意r个行向量线性无关C任意r个行向量都构成极大线性无关向量组D任意一个行向量都可由其他任意r个行向量线性表出
问答题证明： （1）若α(→)1，α(→)2，…，α(→)r是A的属于特征值λ的特征向量，则α(→)1，α(→)2，…，α(→)r的任一个非零线性组合也是A的属于λ的特征向量。 （2）矩阵可逆的充分必要条件是它的特征值都不为0。
单选题设向量组I：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组II：α(→)1，α(→)2，…，α(→)m，β(→)，其秩为s，则r＝s是向量组I与向量组II等价的（ ）。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件
单选题设A，B为满足AB＝0(→)的任意两个非零矩阵，则必有（ ）。AA的列向量组线性相关，B的行向量组线性相关BA的列向量组线性相关，B的列向量组线性相关CA的行向量组线性相关，B的行向量组线性相关DA的行向量组线性相关，B的列向量组线性相关