设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-YB.X+YC.X-2YD.Y-2X
设随机变量X,Y相互独立,且X～N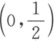
,Y～N
,则与Z=Y-X同分布的随机变量是().
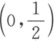,Y～N,则与Z=Y-X同分布的随机变量是().A.X-Y
B.X+Y
C.X-2Y
D.Y-2X
B.X+Y
C.X-2Y
D.Y-2X
参考解析
解析：Z=Y-X～N(1,1)，因为X-Y～N(-1,1),X+Y～N(1,1).X-2Y～N
，Y-2X～N
，所以选(B).
，Y-2X～N，所以选(B).
相关考题：
设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相 关系数为－,又设Z=(1)求E(Z),D(Z)；(2)求；(3)X,Z是否相互独立？为什么？
设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.
设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为 A.A0B.1C.2D.3
填空题已知随机变量X～N（－1，1），Y～N（3，1），且X、Y相互独立，Z＝X－2Y，则Z～____。