按照第三强度理论，图示两种应力状态的危险程度是：A.a)更危险B.b)更危险C.两者相同D.无法判断

按照第三强度理论，图示两种应力状态的危险程度是：



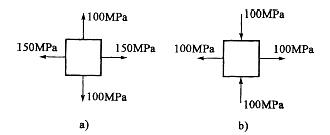
A.a)更危险
B.b)更危险
C.两者相同
D.无法判断

参考解析

解析：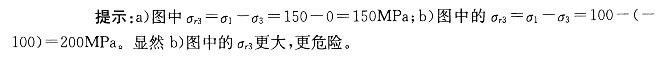

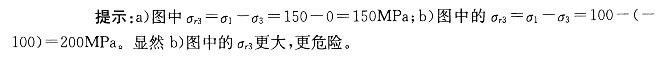
相关考题：

脆性材料无论处于什么应力状态,都应采用第三或第四强度理论,而不能采用第一或第二强度理论。() 此题为判断题(对，错)。
查看答案
若构件内危险点的应力状态为二向等拉,则除()强度理论以外,利用其它三个强度理论进行计算得到的相当应力是相等的。 A.3B.4C.5D.6
查看答案
矩形截面杆承受拉弯组合变形时,因其危险点的应力状态是单向应力,所以不必根据强度理论建立相应的强度条件() 此题为判断题(对，错)。
查看答案
图示点的应力状态，第三强度理论校核该点的强度条件是()，第四强度理论校核该点的强度条件是()。
查看答案
图所示直径为d的实心圆轴，受力如图示，试求：①作轴各基本变形的内力图。②用第三强度理论导出此轴危险点相当应力的表达式。
查看答案
图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是 ()。
查看答案
A.(a)点应力状态较危险B.(b)应力状态较危险C.两者的危险程度相同D.不能判定
查看答案
图示圆轴，在自由端圆周边界承受竖直向下的集中力F，按第三强度理论，危险截面的相当应力σeq3为：
查看答案
折杆受力如图所示，以下结论中错误的为：A.点B和D处于纯剪状态B.点A和C处为二向应力状态，两点处σ1>0,σ2=0,σ3C.按照第三强度理论，点A及C比点B及D危险D.点A及C的最大主应力σ1数值相同
查看答案
图示直径为d的圆轴，承受轴向拉力F和扭矩T。按第三强度理论，截面危险的相当应力σeq3为（　　）。
查看答案
按照第三强度理论，图示两种应力状态的危险程度是（　　）。 A、 无法判断 B、 两者相同 C、 （a）更危险 D、 （b）更危险
查看答案
四种应力状态分别如图所示，按照第三强度理论，其相当应力最大的是：A.状态(1)B.状态(2)C.状态(3)D.状态(4)
查看答案
折杆受力如图示，以下结论中错误的为：(A)点B和D处于纯剪状态(B)点A和C处为二向应力状态,两点处σ1>0,，σ2=0，σ3(C)按照第三强度理论，点A及C比点B及D危险(D)点A及C的最大主应力σ1数值相同
查看答案
图示圆轴，在自由端圆周边界承受竖直向下的集中F，按第三强度理论，危险截面的相当应力σeq3为：
查看答案
四种应力状态分别如图所示，按照第三强度理论，其相当应力最大的是：（A）状态1 （B）状态2（C）状态3 （D）状态4
查看答案
如图5-52所示应力状态，按第三强度理论校核，强度条件为（ ）。
查看答案
折杆受力如图5-64所示，以下结论中错误的为（ ）。A.点B和D处于纯剪切状态B.点A和C处为二向应力状态，两点处σ1>0,σ2=0, σ3C.按照第三强度理论，点A及C比点B及D危险D.点A及C点的最大主应力σ1数值相等
查看答案
两危险点的应力状态如图5-54所示，且由第四强度理论比较其危险程度, 正确答案是为（ ）。 A. (a)应力状态较危险 B. (b)应力状态较危险 C.两者的危险程度相同 D.不能判定
查看答案
第三强度理论，是指（）。A、最大拉应力理论B、最大切应力理论C、最大伸长线应变理论D、畸变能密度理论
查看答案
直径为d的圆轴两端承受转矩m的作用而产生扭转变形，材料的泊松比为ν，其危险点的第一强度理论的相当应力σeq1=（），第二强度理论的相当应力σeq2=（），第三强度理论的相当应力σeq3=（）。
查看答案
对于危险点为二向拉伸应力状态的铸铁构件，应使用（）强度理论进行计算。A、第一B、第二C、第一和第二D、第三和第四
查看答案
第（）强度理论认为，塑性材料屈服破坏的主要原因是最大切应力。A、第一强度理论B、第二强度理论C、第三强度理论D、第四强度理论
查看答案
若构件内危险点的应力状态为二向等拉，则除（）强度理论外，利用其它三个强度理论得到的相当应力是相等的。A、第一B、第二C、第三D、第四
查看答案
矩形截面杆承受拉弯组合变形时，因其危险点的应力状态是单向应力，所以不必根据强度理论建立相应的强度条件。
查看答案
强度理论的适用范围决定于危险点处的应力状态和构件的材料性质。
查看答案
按照塑性理论，构件进入塑性状态的标志是（）。A、截面受拉区边缘的应力到达极限强度B、截面中性轴的应力到达极限强度C、截面受压区边缘的应力到达极限强度D、截面某一点的应力到达极限强度
查看答案
单选题四种应力状态分别如图所示，按照第三强度理论，其相当应力最大的是：（）A状态1B状态2C状态3D状态4
查看答案
热门标签