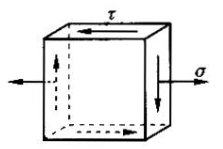
图示点的应力状态,第三强度理论校核该点的强度条件是(),第四强度理论校核该点的强度条件是()。
图示点的应力状态,第三强度理论校核该点的强度条件是(),第四强度理论校核该点的强度条件是()。
相关考题:
利用正应力强度条件,可进行()三个方面的计算。 A.强度校核、刚度校核、稳定性校核B.强度校核、刚度校核、选择截面尺寸C.强度校核、选择截面尺寸、计算允许荷载D.强度校核、稳定性校核、计算允许荷载
折杆受力如图示,以下结论中错误的为:(A)点B和D处于纯剪状态(B)点A和C处为二向应力状态,两点处σ1>0,,σ2=0,σ3(C)按照第三强度理论,点A及C比点B及D危险(D)点A及C的最大主应力σ1数值相同
单选题在零件强度设计时,静应力条件下的塑性材料是以______作为极限应力,而脆性材料是以______作为极限应力。( )A强度极限σb;屈服点σs。B屈服点σs;强度极限σbC强度极限σb;强度极限σsD屈服点σs;屈服点σs;
填空题已知某点的应力状态σly ,该点的应力强度为()。