图示圆轴,在自由端圆周边界承受竖直向下的集中F,按第三强度理论,危险截面的相当应力σeq3为:
图示圆轴,在自由端圆周边界承受竖直向下的集中F,按第三强度理论,危险截面的相当应力σeq3为:

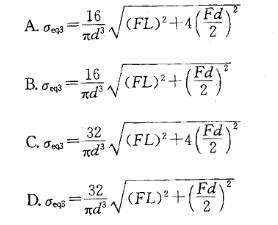

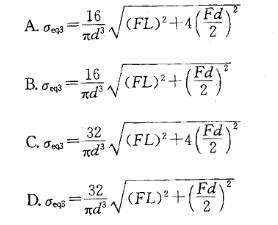
参考解析
解析:提示:把力F沿轴线z平移至圆轴截面中心,并加一个附加力偶,则使圆轴产生弯曲和扭转组合变形。最大弯矩M=Fl,最大扭矩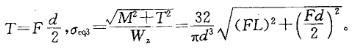
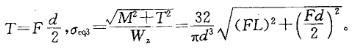
相关考题:
图所示圆截面杆件d=80mm,长度l=1000mm,承受轴向力F1=30kN,横向力F2=1.2kN,外力偶M=700N·m的作用,材料的许用应力[σ]=40MPa,试求:①作杆件内力图。②按第三强度理论校核杆的强度。
图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。已知M=200GPa,μ=0.3,[σ]=140MPa。试求:①作图示圆轴表面点的应力状态图。②求圆轴表面点图示方向的正应变。③按第四强度理论校核圆轴强度。
图示T形截面杆,一端固定一端自由,自由端的集中力F作用在截面的左下角点,并与杆件的轴线平行。该杆发生的变形为:A.绕y和z轴的双向弯曲B.轴向拉伸和绕y、z轴的双向弯曲C.轴向拉伸和绕z轴弯曲D.轴向拉伸和绕y轴弯曲
图示T型截面杆,一端固定一端自由,自由端的集中力F作用再截面的左下角点,并与杆件的轴线平行。该杆发生的变形为:(A)绕y和z轴的双向弯曲 (B)轴向拉伸和绕y、z轴的双向弯曲(C)轴向拉伸和绕z轴弯曲 (D)轴向拉伸和绕y轴弯曲
直径为d的圆轴两端承受转矩m的作用而产生扭转变形,材料的泊松比为ν,其危险点的第一强度理论的相当应力σeq1=(),第二强度理论的相当应力σeq2=(),第三强度理论的相当应力σeq3=()。
多选题以下四种受力构件,需用强度理论进行强度校核的是()。A承受水压力作用的无限长水管B承受内压力作用的两端封闭的薄壁圆筒C自由扭转的圆轴D齿轮传动轴