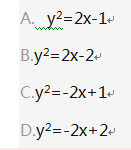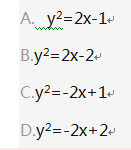已知过点(0,4),斜率为-1的直线l与抛物线C:y2—2px(b>;0)交于A,B两点.(I)求C的顶点到2的距离;(Ⅱ)若线段AB中点的横坐标为6,求C的焦点坐标.
抛物线y2=-4x的准线方程为 ( )A.x=-1B.x=1C.y=1D.Y=-l
(2) 设点P是椭圆C的左准线与 x轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线L的斜率的取值范围。
已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.
抛物线y2=3x的准线方程为 ( )A.AB.BC.CD.D
已知双曲线C:x2/a2-y2/b2=1(a>0,b>0)的一个焦点是抛物线y2=8x的焦点,且双曲线C的离心率为2,那么双曲线C的方程为_______。
(1)求椭圆的标准方程; (2)F2为椭圆的右焦点,过椭圆的中心作一条倾斜角为45°的直线与椭圆交于A、B两点,求△ABF2的面积.
顶点在原点、焦点在χ轴上且通径(过焦点和对称轴垂直的弦)长为6的抛物线方程为_____.
抛物线y2=4x上一点P到焦点F的距离是10,则点P坐标是( )A.(9,6)B.(9,±6)C.(6,9)D.(±6,9)
以抛物线y2=8x的焦点为圆心,且与此抛物线的准线相切的圆的方程是( )A.(x+2)2+y2=16B.(x+2)2+y2=4C.(x-2)2+y2=16D.(x-2)2+y2=4
设直线y=2x+m与抛物线y2=4x没有公共点,则m的取值范围是。
A.B是抛物线y2=8x上两点,且此抛物线的焦点在线段AB上,已知A.B两点的横坐标之和为10,则|AB|=( )A.18 B.14 C.12 D.10
设曲线y=y(x)过(0,0)点,M是曲线上任意一点,MP是法线段,P点在x轴上,已知MP的中点在抛物线,求此曲线的方程。
求过点A(1,-2)的所有直线被圆x2+y2=5截得线段中点的轨迹方程。
椭圆的焦点分别是F1和F2,已知椭圆的离心率.过中心O 作直线与椭圆交于A,B两点,O为原点,若△ABF2的面积是20。 (1)求m的值; (2)直线AB的方程。
点在平面内的运动方程为,则其轨迹为( )。 A.椭圆曲线 B.圆弧曲线 C.直线 D.抛物线
已知M是抛物线y2=2px(p>0)上的点,F是抛物线的焦点,∠FOM=45o,|MF|=2。 (1)求抛物线的方程式;
已知P为抛物线y2=x的焦点,点M,N在该抛物线上且位于x轴的两侧,(其中O为坐标原点),则ΔMPO与ΔNPO面积之和的最小值是( )。
设抛物线y2=2px(p>0)焦点为F,点A坐标为(0,2),若线段FA的中点B在抛物线上,则B到该抛物线准线距离为__________。
过抛物线y2=4x的焦点,倾斜角为45°的直线方程为_______。
已知抛物线y2=2px(p>0),过定点(p,0)作两条互相垂直的直线l1、l2,l1与抛物线交于
曲线方程y2=2px所描述的是()。A、摆线B、渐开线C、双曲线D、抛物线
方程 y2 = 2px(p>0)是抛物线标准方程(SIEMENS系统)。
方程y2=2px(p>0)是抛物线标准方程(FANUC系统、华中系统)。
假定导线的荷载,视为沿直线均匀分布推出的公式称为()。A、平抛物线方程B、斜抛物线方程C、悬链线方程D、状态方程
填空题若直线ax-y+1=0经过抛物线y2=4x的焦点,则实数a=____.
单选题过抛物线y=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程()Ay=2x-1By=2x-2Cy=-2x+1D-2x+2