幂级数的收敛域为( )。
幂级数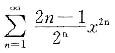 的收敛域为( )。
的收敛域为( )。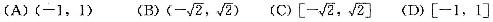
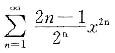 的收敛域为( )。
的收敛域为( )。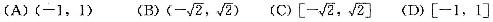
参考解析
解析:令x2=t,幂级数化为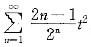
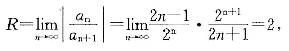 当|t|<2,即|x2|<2,亦即
当|t|<2,即|x2|<2,亦即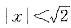 时收敛,而当
时收敛,而当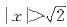 发散,而当
发散,而当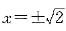 时,级数∑(2n-1)发散,从而原级数的收敛域为
时,级数∑(2n-1)发散,从而原级数的收敛域为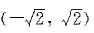
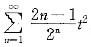
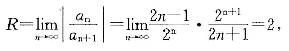 当|t|<2,即|x2|<2,亦即
当|t|<2,即|x2|<2,亦即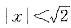 时收敛,而当
时收敛,而当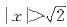 发散,而当
发散,而当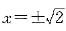 时,级数∑(2n-1)发散,从而原级数的收敛域为
时,级数∑(2n-1)发散,从而原级数的收敛域为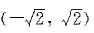
相关考题:
序列的收敛域描述正确的是________。 A.对于有限长的序列,其双边z变换在整个平面B.对因果序列,其z变换的收敛域为某个圆外区域C.对反因果序列,其z变换的收敛域为某个圆外区域D.对双边序列,其z变换的收敛域为环状区域
单选题序列的收敛域描述错误的是():A对于有限长的序列,其双边z变换在整个平面B对因果序列,其z变换的收敛域为某个圆外区域C对反因果序列,其z变换的收敛域为某个圆外区域D对双边序列,其z变换的收敛域为环状区域
单选题在原点展开的幂级数的收敛域一定是()。A有界区域B关于原点对称的区域C无界区域D由正数组成的区域