固定铰支座处的截面有() A、水平约束反力B、竖向约束反力C、约束力矩D、水平位移E、转角位移
图示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B端转角为:A.θ,顺时针B.θ,逆时针C.θ/2,顺时针D.θ/2,逆时针
图示结构,当支座B发生沉降Δ时,支座B处梁截面的转角大小为:
图示结构EI=常数,当支座A发生转角θ支座B处截面的转角为(以顺时针为正)( )。A.θ/3B.2θ/5C.-θ/3D.-2θ/5
如图所示的结构中,B支座发生支座移动,D点水平位移(向右为正)为( )。
图示梁AB,EI为常数,固支端A发生顺时针的支座转动,由此引起的B处的转角为( )。
图示刚架,EI为常数,忽略轴向变形。当D支座发生支座沉降时,B点转角为( )。
如图所示的一三铰刚架,其右支座发生了位移,位移的水平分量为Δ1,竖向分量为Δ2,则右半部的转角为( )。
图示梁线刚度为i,长度为ι,当A端发微小转角α,B端发生微小位△ια时,梁两端弯矩(对杆端顺时针为正)为( )。
图示结构A点的竖向位移(向下为正)为( )。A、aB、bC、cD、d
图所示结构,各杆,当支座B发生图示的移动时,结点E的水平位移为( )。
图示结构支座A下沉了d并发生了顺时针方向转角α,当用力法计算并取图(b)为基本结构时,力法方程应为( )。
图示结构支座B发生了移动,则点C的竖向位移( )。{图1}
图示结构EI=常数,当支座B发生沉降Δ时,支座B处梁截面的转角为(以顺时针为正)( )。A、Δ/lB、1、2Δ/lC、1、5Δ/lD、Δ/2l
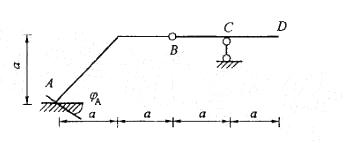
如图所示结构,支座A发生了位移θA=α,铰C左、右两侧的相对转角θ为( )。
图示各种结构中,欲求A点竖向位移,能用图乘法的为:
图示结构用位移法计算时,若取结点A的转角为Z1(顺时针),则为r11( )。
图示结构当E点有P=1向下作用时,B截面产生逆时针转角φ,则当A点有图示荷载作用时,E点产生的竖向位移为:A.φ↑ B.φ↓ C. φa ↑D. φa↓
图示梁和常数,固定端A发生顺时针方向角位移θ,则铰支端B的转角(以顺时针方向为正)为:( )A.θ/2B.θC.-θ/2D.-θ
如图所示。支座B发生了移动,则点C的竖向位移为( )。
A.水平位移B.竖向位移C.水平位移+转角D.水平位移+竖向位移+转角
图示结构当支座B有沉降时会产生() A 内力B 反力C 位移D 变形
单选题图示结构El=常数,当支座B发生沉降△时,支座B处梁截面的转角为(以顺时针为正)( )。A △/lB 1.2△/lC 1.5△/lD △/2l