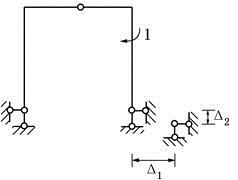
如图所示的一三铰刚架,其右支座发生了位移,位移的水平分量为Δ1,竖向分量为Δ2,则右半部的转角为( )。
如图所示的一三铰刚架,其右支座发生了位移,位移的水平分量为Δ1,竖向分量为Δ2,则右半部的转角为( )。
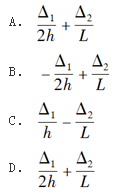

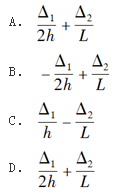
参考解析
解析:在右半部分结构上虚设一单位力偶,可得支座反力如图所示。
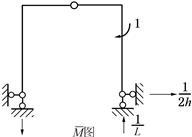
故右半部分转角
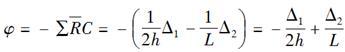

故右半部分转角
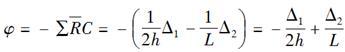
相关考题:
力的做功在我们生活中很常见。当有一力F作用于一物体,物体位移为S,力F在位移方向有个分量F1,在位移垂直方向有一个力的分量F2.则力F对该物体做的功为()。A、F*SB、F1*SC、F2*SD、以上都不是
单选题力的做功在我们生活中很常见。当有一力F作用于一物体,物体位移为S,力F在位移方向有个分量F1,在位移垂直方向有一个力的分量F2.则力F对该物体做的功为()。AF*SBF1*SCF2*SD以上都不是