如图13所示梁B点处的竖向位移( )。A、向下B、为0C、可能向下也可能向上D、向上
图示结构,EI=常数,截面高h=常数,线膨胀系数为a,外侧环境温度降低t°C,内测环境温度升高t°C,引起的C点竖向位移大小为:
图示刚架材料的线膨胀系数为α,各杆截面均为矩形,截面高度为h,由于图示温度变化引起C点的竖向位移为( )。
图示结构,EI=常数,截面高h=常数,线膨胀系数为α,外侧环境温度降低t℃,内侧环境温度升高t℃,引起的C点竖向位移大小为( )。
如图所示组合结构,梁式杆件EI=常数,桁架杆件EA=常数,C点竖向位移为( )。 A、向上 B、向下 C、为零 D、需计算确定
图示梁自重不计,在集中重量W作用下,C点的竖向位移Δc =1cm,则该体系的自振周期为:A. 0.032sB. 0.201sC. 0. 319sD. 2. 007s
图示桁架K点的竖向位移为最小的图为( )。A、AB、BC、CD、D
图示结构,EI为常数。结点B处弹性支撑刚度系数k=3EI/L3,C点的竖向位移为( )。
图示结构A点的竖向位移(向下为正)为( )。A、aB、bC、cD、d
图示结构支座B发生了移动,则点C的竖向位移( )。{图1}
图示梁自重不计,在集中重量W作用下,C点的竖向位移Δc =1cm,则该体系的自振周期为:A. 0.032s B. 0.201s C. 0. 319s D. 2. 007s
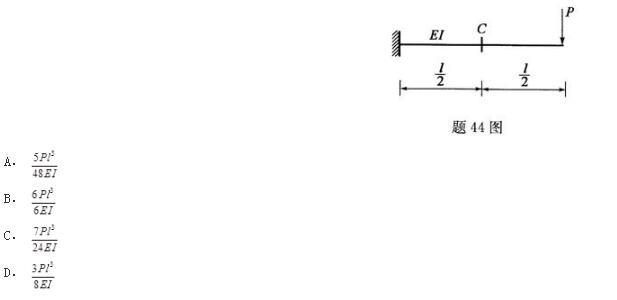
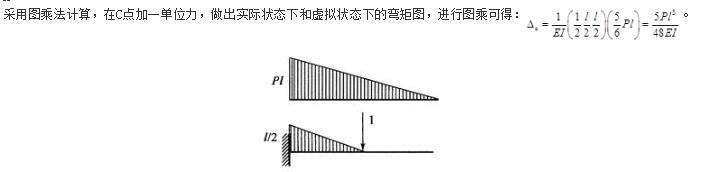
图示各种结构中,欲求A点竖向位移,能用图乘法的为:
图示结构,各杆EI、EA相同,C点的竖向位移应:A.向上 B.向下 C.为零 D.不能确定
图示结构,当支座A发生顺时针转角φA时,D点的竖向位移为:A.φAa,向下 B. φAa,向上 C.2φAa,向下 D.2φAa,向上
图示结构当E点有P=1向下作用时,B截面产生逆时针转角φ,则当A点有图示荷载作用时,E点产生的竖向位移为:A.φ↑ B.φ↓ C. φa ↑D. φa↓
图示桁架的所有杆件EA值均相同,则桁架A点的竖向位移最小的是( )。A.B.C.D.
图示连续梁由于地基沉降,在C点有一向下位移△,以下可能的连续梁变形情况是( )。A.B.C.D.
图示结构所有杆件EA均相同,则A点竖向位移最大的是( )。A.B.C.D.
图示桁架的杆件长度和材质均相同,K点的竖向位移最小的是:( )A.B.C.D.
图示为梁的虚设力状态,按此力状态及位移计算公式可求出AB两点的相对线位移。 A对B错
为建立双肢墙连梁未知竖向剪力q(x)的微分方程,需要分析连梁跨中切口处的竖向变形协调条件,切口处的竖向相对位移由三部分组成,其中不包括()A、连梁的轴向变形产生的竖向相对位移B、墙肢弯曲变形产生的竖向相对位移C、墙肢的轴向变形产生的竖向相对位移D、连梁的弯曲变形和剪切变形产生的竖向相对位移
单选题为建立双肢墙连梁未知竖向剪力q(x)的微分方程,需要分析连梁跨中切口处的竖向变形协调条件,切口处的竖向相对位移由三部分组成,其中不包括()A连梁的轴向变形产生的竖向相对位移B墙肢弯曲变形产生的竖向相对位移C墙肢的轴向变形产生的竖向相对位移D连梁的弯曲变形和剪切变形产生的竖向相对位移