函数y= (5-x)x(2/3)的极值可疑点的个数是：A.0B. 1C. 2D. 3

函数y= (5-x)x(2/3)的极值可疑点的个数是：

A.0
B. 1
C. 2
D. 3

参考解析

解析：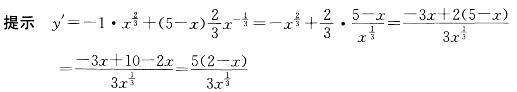
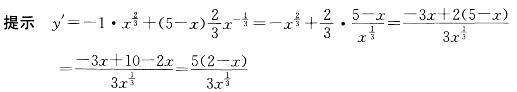
可知x=0，x=2为极值可疑点。所以极值可疑点的个数为2。

相关考题：

以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
查看答案
(本题满分8分)求函数y＝x3-3x2-1的单调区间、极值及其曲线的凹凸区间和拐点。
查看答案
求函数y=x3-3x2-9x＋1的极值．
查看答案
数学理解有一组数同时适合方程 x+y=2和 x+y=5吗？一次函数y=2-x，y=5-x的图像之间有何关系？你能从中“悟”出些什么吗？
查看答案
求二元函数(x，y)=x2+y2+xy在条件x+2y=4下的极值．
查看答案
确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点．
查看答案
求函数z=x2+2y2+4x-8y+2的极值．
查看答案
求函数(x，y)=x2+y2在条件2x+3y=1下的极值．
查看答案
设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．
查看答案
求y=f(x)=2x3-3x2-12x+14的极值点和极值，以及函数曲线的凸凹性区间和拐点.
查看答案
求函数z=x2+y2+2y的极值．
查看答案
求函数z=x2-xy+y2+9x一6y+20的极值．
查看答案
求函数(x，y)=4(x-y)-x2-y2的极值．
查看答案
已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值.
查看答案
设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.
查看答案
求二元函数f(x，y)=x^2(2+y^2)+ylny的极值.
查看答案
若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。A. f(x,y)的极值点一定是f(x,y)的驻点B.如果P0是f(x,y)的极值点，则P0点处B2-AC)C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0D.f(x,y)的最大值点一定是f(x,y)的极大值点
查看答案
求函数f(x，y)=e2x(x+y2+2y)的极值.?
查看答案
点（2，-2）是函数f（x，y）=x（4―x）―y（y+4）的（）。A、极小值点B、非极值点C、非极值驻点D、极大值点
查看答案
下列各点中为二元函数z=x3-y3-3x2+3y-9x的极值点的是（）。A、（3，-1）B、（3，1）C、（1，1）D、（-1，-1）
查看答案
若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。A、f（x，y）的极值点一定是f（x，y）的驻点B、如果P0是f（x，y）的极值点，则P0点处B2-AC0C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0D、f（x，y）的最大值点一定是f（x，y）的极大值点
查看答案
函数少=（5_X）X3的极值可疑点的个数是（）。A、0B、1C、2D、3
查看答案
问答题求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。
查看答案
单选题函数少=（5_X）X3的极值可疑点的个数是（）。A0B1C2D3
查看答案
单选题点（2，-2）是函数f（x，y）=x（4―x）―y（y+4）的（）。A极小值点B非极值点C非极值驻点D极大值点
查看答案
单选题（2010）下列各点中为二元函数z=x3-y3-3x2+3y-9x的极值点的是：（）A（3，-1）B（3，1）C（1，1）D（-1，-1）
查看答案
单选题函数y＝（5－x）x2/3的极值可疑点的个数是（　　）。[2013年真题]A0B1C2D3
查看答案
热门标签