下列矩阵所对应的线性变换为关于y=-x的对称变换的是( )。
下列矩阵所对应的线性变换为关于y=-x的对称变换的是( )。
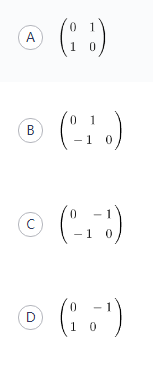
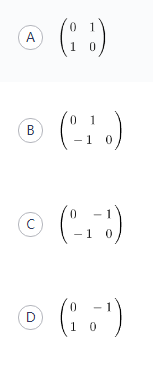
参考解析
解析:

相关考题:
使用下列二维图形变换矩阵:T =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001010 产生图形变换的结果为 ( )A绕原点逆时针旋转90度;B以Y=X 为对称轴的对称图形;C以Y=-X 为对称轴的对称图形;D绕原点顺时针旋转90度。
使用下列二维图形变换矩阵A=a*T,,其中,a是行向量(xy1),是齐次坐标形式的二维点。给定的变换矩阵T如下所示,则将产生的变换结果为()A.图形放大2倍B.图形放大2倍,同时沿X、Y坐标轴方向各移动一个单位C.沿X坐标轴方向各移动2个单位D.沿X坐标轴放大2倍,同时沿X、Y坐标轴方向各移动一个单位
n*n矩阵可看作是n维空间中的线性变换,矩阵的特征向量经过线性变换后,只是乘以某个常数(特征值),因此,特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1,w2,w3),其对应的特征值为( )。A.1/3B.1C.3D.9
利用3×3矩阵进行二维点集变化时,我们使用的矩阵为[1,0,0;0,-1,0;0,0,1],那么变化后的效果为()A、沿着X轴对称变换B、沿着Y轴对称变换C、沿着原点对称变换D、沿着直线y=x对称变换
关于对称分量变换、dq0、MT0、120变换,正确的说法有()A、对称分量变换前后的物理量为相量B、dq0变换为相量变换C、对称分量变换、120变换具有相同的变换矩阵D、MT0变换专用于同步电机分析
多选题采用齐次坐标来实现图形变换的优点是()A既可使矩阵变换满足结合率也可使矩阵变换满足交换率。B所有的图形变换都可以用矩阵乘法来实现。C可使矩阵变换满足结合率但不满足交换率。D可使非线性变换也能采用线性变换来实现。E可方便地实现任意的图形变换组合。F所有的图形变换都可以用矩阵加法来实现。
单选题利用3×3矩阵进行二维点集变化时,我们使用的矩阵为[1,0,0;0,-1,0;0,0,1],那么变化后的效果为()A沿着X轴对称变换B沿着Y轴对称变换C沿着原点对称变换D沿着直线y=x对称变换
单选题图形的二维变换包括平移变换、比例变换、旋转变换、错切变换和()A线性变换B对称变换C扫描变换D拉伸变换