若线性方程组无解,则数k等于( )。A.6B.4C.3D.2
若线性方程组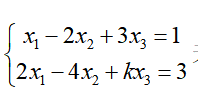 无解,则数k等于( )。
无解,则数k等于( )。
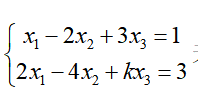 无解,则数k等于( )。
无解,则数k等于( )。A.6
B.4
C.3
D.2
B.4
C.3
D.2
参考解析
解析:本题考查非齐次线性方程组解的情况与增广矩阵和系数矩阵之间的关系。非齐次线性方程组无解,
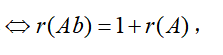
由此可得k=6。
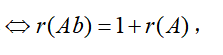
由此可得k=6。
相关考题:
若x值的均数等于7,标准差等于2,则x+3的均数A.也等于7B.等于9C.等于l0 若x值的均数等于7,标准差等于2,则x+3的均数A.也等于7B.等于9C.等于l0D.界于7—3与7+3之间E.界于7—1.96×2与7+1.96×2之间
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3,且η1,η2,η3是3个不同的解向量,则通解是( ).A.x=k1(η-η2)+η3B.x=k1η1+k2η2+η3C.x=k1η1+k2η2+k3η3D.x=k1(η+η2)+η3
单选题用单纯形法求解极大化线性规划问题中,若某非基变量检验数为零,而其他非基变量检验数全部0,则说明本问题()。A有惟一最优解B有多重最优解C无界D无解