人教版七年级数学下册第六章 实数练习（含答案）
数学理解
1，2，3，4，5，6，7，8，9，10的平方根和立方根中，哪些是有理数？哪些是无理数？
平方根是有理数：1,4,9
立方根是有理数：1,8
平方根是无理数：2,3,5,6,7,8,10
立方根是无理数：2,3,4,5,6,7,9,10
判断题：
（1）不带根号的数都是有理数；
（2）两个无理数的和还是无理数。
(1)错 (2)错
“无理数就是开方开不尽的数”这句话对吗？请举例说明。
错
无理数：无限不循环小数
特征：（1）无理数的小数部分位数无限
（2）无理数的小数部分不循环，不能表示成分数
举例：（1）开方开不尽的数，如
（2）含有π的一类数
（3）以无限不循环小数的形式出现的特定结构数
你能举出一些有关无理数的实例吗？
圆形面积；
面积为5的正方形边长…
数学理解
两个有理数相加、相减、相乘、相除，结果一定还是有理数吗？说明理由，两个无理数相加、相减、相乘、相除，结果一定还是无理数吗？举例说明。
两个有理数相加、相减、相乘、相除，结果一定还是有理数！
两个无理数相加、相减、相乘、相除，结果不一定是无理数！
第六章 实数一、单选题19的算术平方根是（）A3B3CD2下列说法中正确的说法的个数为( )（1）无理数就是开方开不尽的数；（2）无理数是无限小数；（3）无理数包括正无理数,零,负无理数；（4）无理数都可以用数轴上的点来表示.A1B2C3D43面积为4的正方形的边长是（ ）A4的平方根B4的算术平方根C4开平方的结果D4的立方根4的立方根是（ ）A4B2C-2D-45若一个数的平方根是8，那么这个数的立方根是（）A2B4C4D26下列式子中，正确的是（）A38=2B3.6=0.6C(2)2=2D36=67实数a，b在数轴上的对应点的位置如图所示把a，b，0按照从小到大的顺序排列，正确的是（）Aa0bB0abCb0aDba08下面是一组按规律排列的数，第个数应是（ ）ABCD以上答案均不对9估计5的值应在（）A5和6之间B6和7之间C7和8之间D8和9之间10若x4，则x的取值范围是()A2x3B3x4C4x5D5x6二、填空题11计算：_12一个数的立方根是，则这个数的算术平方根是_.13请先观察下列算式，再填空：321281，523282，725283，927284通过观察归纳，写出第2020个算式是：_14比较大小：_（选填“”“”或“”）三、解答题15已知一个正数的两个不相等的平方根是a+6与2a9（1）求a的值及这个正数；（2）求关于x的方程ax2160的解16已知 2x-1 的算术平方根是 3，y+3 的立方根是-1，求代数式 2x+y 的平方根17解下列方程（1） （2）18计算（1） （2）19若一个四位自然数满足个位与百位相同，十位与千位相同，我们称这个数为“双子数”.将“双子数”的百位、千位上的数字交换位置，个位、十位上的数字也交换位置，得到个新的双子数，记为“双子数”的“双11数”.例如，则.（1）计算2424的“双11数”_；（2）若“双子数”的“双11数”的是一个完全平方数，求的值；（3）已知两个“双子数”、，其中，（其中，且、都为整数，若的“双11数”能被17整除，且、的“双11数”满足，令，求的值答案1B2B3B4C5C6A7B8C9C10A11512134041240392820201415（1）a1，这个正数是49；（2）x4或x41617（1）x= 或x=-；（2）x=-18（1）-5（2）19（1）12；（2）4或16或36；（3）51或17
0，1，2，3，4，5，6，7，8，9，10的平方根及立方根中，哪些是有理数？哪些是无理数？
（1）0,1,4,9的平方根是有理数
（2）2,3,5,6,7,8,10的平方根是无理数
（3）0,1,8的立方根是有理数
（4）2,3,4,5,6,7,9,10 的立方根是无理数
判断下列说法是否正确：
（1）无限小数都是无理数；
（2）无理数都是无限小数；
（3）带根号的数都是无理数；
（4）所有有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；
（5）所有实数都可以用数轴上的点表示，反过来，数轴上的所有点都表示实数。
（1）错误
（2）正确
（3）错误
（4）错误
（5）正确
（1）有没有最小的正整数？有没有最小的整数？
（2）有没有最小的有理数？有没有最小的无理数？
（3）有没有最小的正实数？有没有最小的实数？
解：（1）有最小的正整数1，没有最小的整数；
（2）没有最小的有理数，没有最小的无理数；
（3）没有最小的正实数，没有最小的实数。
所有的有理数都是实数；所有的无理数也是实数；虚数不是实数。因此，虚数既不是有理数也不是无理数．
(1)将上述命题符号化。
(2)用演绎法证明其结论是否正确。
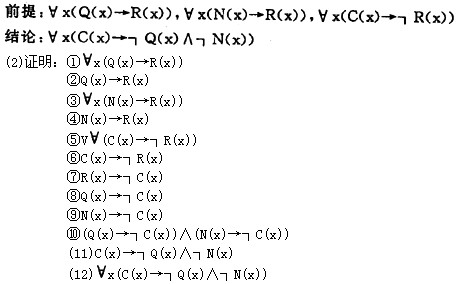所以结论是正确的。设Q(x):x是有理数； R(x):x是实数； N(x):x是无理数； C(x):x是虚数。 则命题可符号为：
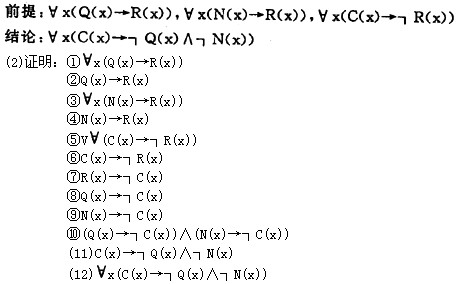所以结论是正确的。
写出一个大于1且小于4的无理数 ．
相关考题：
- 多选题患者女，45岁，因“进行性加重性心悸、气短、不能平卧2周”来诊。患者左侧乳腺癌病史3年。超声心动图检查时应关注（）。（提示ECG://频发房性期前收缩。）A各房室大小B室壁厚度和运动幅度C各瓣膜形态和活动D心包内有无异常回声E心腔内有无异常回声F有无肺动脉高压G有无异常血流信号
- 单选题According to the writer, the linguistic insularity of British businesses ______.Alater spread to other countries.Bhad a negative effect on their business.Cexsisted as a problem in 1960s.Dmade non-English-speaking companies turn to other markets.
- 单选题甲厂生产一种易拉罐装碳酸饮料。消费者丙从乙商场购买这种饮料后，在开启时被罐内强烈气流炸伤眼部。下列答案中最正确的是（）。A丙只能向乙索赔B丙只能向甲索赔C丙只能向消费者协会投诉，请其确定向谁索赔D丙可向甲、乙中的任何一方索赔
- 单选题Regular part-time work is ______.Aalways easily found.Bnot always available.Csufficient to pay for tuition fees.D20 hours during full-time vacation.
- 单选题“春眠不觉晓”，这种逍遥，自古以来就是“悠闲阶级”独享和提倡的情怀和境界。今天看来，特别对处于竞争激烈环境下的现代人来讲，（）。A只有欣赏的心情了B只能是一种奢望了C只有在周末享受了D只是孩时的记忆了
- 单选题Evaluate the following query: SQL SELECT TRUNC(ROUND(156.00,-1),-1)FROM DUAL; What would be the outcome?（）A16 B100 C160 D200 E150
- 多选题Which two statements are true about encrypting RMAN backup?（）AThe transparent encryption of backups uses the encryption walletBThe database uses the same encryption key for every encrypted backupCThe password encryption of backups only uses the password while creating and restoring backupDIf transparent encryption is configured, you cannot use the SET ENCRYPTION BY PASSWORD command to make password-protected backups.
- 多选题You are working on a CATDB database that contains an Oracle Database version 11.1 catalog schema owned by the user RCO11. The INST1 database contains an Oracle Database version 10.1 catalog schema owned by the user RCAT10. You want the RMAN to import metadata for database IDs 1423241 and 1423242, registered in RCAT10, into the recovery catalog owned by RCO11. You executed the following RMAN commands: RMAN CONNECT CATALOG rco11/password@catdb RMAN IMPORT CATALOG rcat10/oracle@inst1; What happens when you execute the above commands?（）AThey deregister all databases registered in the RCAT10 catalog.BThey import metadata for all registered databases in the RCAT10 database.CThey register all the RCAT10-catalog registered databases in the RCO11 catalog.DThey overwrite all stored scripts in the RCO11 catalog with the same name as that in the RCAT10 catalog.
- 单选题委托处置行收到委托处置资产的收回款项后，如果处置所得款项小于委托处置资产表内本息账面余额，差额（）。A计入待处理委托资产处置损失科目B计入应付财政部表外收回款项科目C在原科目核算，继续向债务人索取D和委托基金科目对冲抵消
- 多选题Which tasks are run automatically as part of the Automated Maintenance Task by default?（）ASegment AdvisorBSQL Access AdvisorCOptimizer statistics gatheringDAutomatic SQL Tuning AdvisorEAutomatic Database Diagnostics Monitor