高考数学复习专题21《利用导数解决函数的恒成立问题》讲义及答案
已知集合A={x|x≤1},B={x|≥a},且A∪B=R,
则实数a的取值范围是__________________.
2.ɑ≤1
若对于任意实数x,都有t2+5t ≤|2x-4|-|x+2|恒成立,则t的取值范围是( ).
(A)[1,4].
(B)[-4,-1].
(C)(-∞,1]∪[4,+∞).
(D)(-∞,-4]∪[-1,+∞).
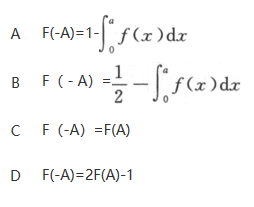

B.(-∞,1)
C.(1,+∞)
D.(-∞,+∞)

专题21 利用导数解决函数的恒成立问题一、单选题 1已知,为实数,不等式恒成立,则的最小值为( )ABC1D22已知函数,且,当时,恒成立,则a的取值范围为( )ABCD3已知函数(,且),对任意,不等式恒成立,则实数a的最小值是( )ABeC3D24对于正数,定义函数:.若对函数,有恒成立,则( )A的最大值为B的最小值为C的最大值为D的最小值为5已知函数,若任意,且都有,则实数的取值范围( )A,B,C,D6已知函数,若对,恒成立,则整数的最小值为( )A1B2C3D47已知,若对任意正实数,都有,则的取值范围是( )ABCD二、解答题8已知函数.(1)若曲线与直线相切,求的值;(2)若存在,使成立,求实数的取值范围.9已知函数,其中,均为实数(1)试判断过点能做几条直线与的图象相切,并说明理由;(2)设,若对任意的,(),恒成立,求的最小值10已知函数,其中(1)求的极值;(2)设,当时,关于的不等式在区间上恒成立,求的最小值11已知函数(1)当时,求的值;(2)当时,关于x的不等式恒成立,求实数a的取值范围12已知函数(1)求函数在上的最小值;(2)若,求实数的值13函数.(1)当时,求的单调区间;(2)当时,恒成立,求整数的最大值.14已知函数,(1)若的最大值是0,求的值;(2)若对其定义域内任意,恒成立,求的取值范围15已知函数,且恒成立(1)求实数的值;(2)记,若,且当时,不等式恒成立,求的最大值16已知函数.(1)当时,求的最小值;(2)若对任意恒有不等式成立.求实数的值;证明:.17已知函数.(1)设,求函数的单调区间;(2)若,且当时,恒成立,试确定的取值范围.18已知函数 (1)如果函数f(x)的单调递减区间为,求f(x)的表达式; (2)若不等式恒成立,求实数a的取值范围.19已知函数.(1)当时,求函数的在(3,)处的切线方程;(2)若函数在其图象上任意一点处切线的斜率都小于,求实数的取值范围.20已知,函数.(1)若,求曲线在处的切线方程;(2)若当时,求的所有可能取值.21设函数.(1)若,求的单调区间;(2)若时,求的取值范围.22已知函数f(x)=-mx-2,g(x)=-sinx- xcosx-1.(1)当x时,若不等式f(x) 0恒成立,求正整数m的值;(2)当x0时,判断函数g(x)的零点个数,并证明你的结论,参考数据: 4.823已知函数.(1)求曲线在点(1,)处的切线方程;(2)若对恒成立,求的最小值.24已知函数在处有极值.(1)求的值,并判断是的极大值点还是极小值点?(2)若不等式对于任意的恒成立,求的取值范围.25已知函数,且在处取得极值()求b的值;()若当时,恒成立,求c的取值范围;()对任意的,是否恒成立?如果成立,给出证明;如果不成立,请说明理由26设函数.(1)求函数的单调区间;(2)若函数在处取得最大值,求a的取值范围.27已知函数(1)当时,若函数在其图象上任意一点处的切线斜率为,求的最小值,并求此时的切线方程;(2)若函数的极大值点为,恒成立,求的范围28已知函数,.(1)若曲线在处的切线与直线垂直,求实数的值;(2)设,若对任意两个不等的正数,都有恒成立,求实数的取值范围;(3)若上存在一点,使得成立,求实数的取值范围.29已知函数.(1)讨论函数的单调性;(2)若,函数在上恒成立,求证:.30已知函数.(1)若函数,求函数的极值;(2)若在时恒成立,求实数的最小值.专题21 利用导数解决函数的恒成立问题一、单选题 1已知,为实数,不等式恒成立,则的最小值为( )ABC1D2【答案】B【分析】不等式恒成立,设,即恒成立,求出,分析得出函数的单调区间,求出函数的最大值,从而可得,即,设,求出的最小值即可得出答案.【详解】设,则恒成立等价于成立,显然时不合题意当时,当时,当时,则在上单调递增,在上单调递减,令,则,当时,在上单调递减,当时,在上单调递增,此时,故选:B【点睛】关键点睛:本题考查利用导数解决范围问题,求解本题的关键有两点:一是对问题进行等价转化,即设,恒成立等价于成立初步判断出的取值范围;二是求出之后,构造函数,利用导数求函数的最小值,进而求得的最小值属于难题.2已知函数,且,当时,恒成立,则a的取值范围为( )ABCD【答案】B【分析】由,可得,从而,从而当时,恒成立,构造函数,可得,结合时,取得最大值1,从而的最大值为,只需即可.【详解】由题意,解得,则,则当时,即恒成立,令,则,当时,时,所以在上是减函数,在是增函数,又因为当时,取得最大值1,所以当时,取得最大值,所以.故选:B.【点睛】关键点点睛:本题考查不等式恒成立问题,解题关键是将原不等式转化为,进而求出的最大值,令其小于即可.考查学生的逻辑推理能力,计算求解能力,属于中档题.3已知函数(,且),对任意,不等式恒成立,则实数a的最小值是( )ABeC3D2【答案】A【分析】由导数求得在上单调递增,求得函数的最值,把任意,不等式 恒成立,转化为,进而求得的取值范围,得到最小值.【详解】由题意,显然,因为函数,可得,又由,可得,故,函数在上单调递增,故,对任意,不等式恒成立,即,所以,即,解得,即实数的最小值为.故选:A.【点睛】对于利用导数研究不等式的恒成立问题的求解策略:1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题4对于正数,定义函数:.若对函数,有恒成立,则( )A的最大值为B的最小值为C的最大值为D的最小值为【答案】B【分析】利用导数求出函数的最大值,由函数的定义结合恒成立可知,由此可得出的取值范围,进而可得出合适的选项.【详解】对于正数,定义函数:,且恒成立,则.函数的定义域为,且.当时,此时,函数单调递增;当时,此时,函数单调递减.所以,.因此,的最小值为.故选:B.【点睛】解决导数中的新定义的问题,要紧扣新定义的本质,将问题转化为导数相关的问题,本题将问题转为不等式恒成立,从而将问题转化为求函数的最大值.5已知函数,若任意,且都有,则实数的取值范围( )A,B,C,D【答案】A【分析】求出函数的导数,通过讨论的范围,得到关于的不等式,解出即可【详解】表示函数在区间上任意两个不同点连线的斜率都大于,等价于,时恒成立,时,不合题意,时,只需,即在,恒成立,故,故的范围是,故选:A【点睛】表示函数在区间上任意两个不同点连线的斜率都大于,由此考虑利用导数进行求解.6已知函数,若对,恒成立,则整数的最小值为( )A1B2C3D4【答案】B【分析】,问题变形为在上恒成立设,用导数求出它的最大值,对最大值估计其范围后可得的最小整数值【详解】即为,因为,所以,即在上恒成立设,则,令,则在上是增函数,所以在上存在唯一零点,即,所以时,递增,时,递减,所以,所以,又,所以的最小整数值为2故选:B【点睛】关键点点睛:本题考查不等式恒成立问题,解题方法用分离参数法变形为求函数最大值,在求函数最大值时,导函数的零点需要定性分析,估计出范围,利用零点求出函数的最大值,再得出最大值的范围,然后得出所求结论7已知,若对任意正实数,都有,则的取值范围是( )ABCD【答案】B【分析】根据条件可变形为,构造函数,利用其为增函数即可求解.【详解】根据可知,令由知为增函数,所以恒成立,分离参数得,而当时,在时有最大值为,故.故选:B.【点睛】关键点点睛:本题由条件恒成立,转化为恒成立是解题的关键,再根据此式知函数为增函数,考查了推理分析能力,属于中档题.二、解答题8已知函数.(1)若曲线与直线相切,求的值;(2)若存在,使成立,求实数的取值范围.【答案】(1)1;(2).【分析】(1)利用切点和切线的斜率列方程,由此求得的值.(2)将已知条件转化为存在,使成立,构造函数,利用导数研究的单调性和最值,结合对进行分类讨论,由此求得的取值范围.【详解】(1)设切点坐标为,因为,所以,又,所以,故,所以.(2)存在,使成立,等价于:存在,使成立.令,令,当时,故在单调递增,所以,当时,故在单调递增,所以,由已知,即.当时,故存在,使得.此时.若时,;若时,.所以,令,所以在单调递增,所以;所以,故.令,故在单调递增,所以,故故不存在,使成立.综合上述:实数的取值范围是.【点睛】解决导数与切线的问题,关键把握住切点和斜率,切点既在切线上,也在原函数图象上.9已知函数,其中,均为实数(1)试判断过点能做几条直线与的图象相切,并说明理由;(2)设,若对任意的,(),恒成立,求的最小值【答案】(1)2条,理由见解析;(2).【分析】(1)设切线方程为,切点为,根据导数的几何意义和斜率公式,得到方程所以得,根据方程显然有两个不等的实根,即可作出判定;(2)把不等式转化为,进而转化为恒成立,设,利用导数求得函数的单调性与最值,即可求解.【详解】(1)设过点与图象相切的直线方程为,切点为,由函数,可得,则,所以得,因为,此方程显然有两个不等的实根,所以过点能做2条直线与的图像相切(2)当时,因为在恒成立,所以在上为增函数,设,所以在恒成立,所以在上为增函数,设,则等价于,即,设,则在为减函数,在上恒成立,恒成立设,为减函数,在上的最大值为,的最小值为【点睛】对于利用导数研究不等式的恒成立问题的求解策略:1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题3、根据恒成求解参数的取值时,一般涉及分类参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,通常要设出导数的零点,难度较大.10已知函数,其中(1)求的极值;(2)设,当时,关于的不等式在区间上恒成立,求的最小值【答案】(1)当时,的极大值为,无极小值;当时,的极大值为,极小值为;(2).【分析】(1)对函数求导,通过分类讨论来判断导

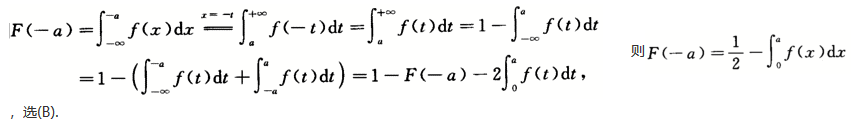
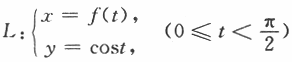 ,其中函数f(t)具有连续导数,且f(0)=0,f'(t)>0(0
,其中函数f(t)具有连续导数,且f(0)=0,f'(t)>0(0



相关考题:
- Response对象的()方法可以将缓冲区中的页面内容立即输出到客户端。A. WriteB. EndC. ClearD. Flush
- 每一笔贷款只能展期一次.
- 小张毕业后进入了一家广告公司,凭着过硬的专业素质和不懈的努力很快成为公司的业务骨干,并被提拔为部门经理。但让公司领导略感意外的是,小张升为主管后虽然依然工作勤恳,但他所管理的部门的整体业绩反而较先前有所下降。通过私下询问,员工们普遍反映小张对下属缺乏适当的管理和激励,他似乎并不关心下属的工作绩效问题。问题一:从小张的表现可以看出,他具有较高的( )。 A.亲和需要 B.安全需要 C。权力需要 D.成就需要问题二:具有小张这种较高需要的入,通常有以下特点( )。 A.责任感较弱 B。希望别人顺从自己的意志 C。喜欢得到及时的反馈情况 D.经常选择做有适度风险的工作问题三:根据麦克里兰提出的需要理论,亲和需求高的人常常( )。A。不易受他人影响 B。在组织中充当管理者的角色 C。看重能否被他人接受 D.喜欢能体现其地位的场合
- 可以自由兑换其他国家货币的外汇称为现汇.
- 形位公差带形状是距离为公差值t的两平行平面内区域的有()A.平面度B.任意方向的线的直线度C.圆柱度D.任意方向的线的位置度
- 《论持久战》一书发表于1945年
- 根据马斯洛的需要层次理论,获得友好和睦的同事关系的需要属于( )。A。生理需要 B.安全需要 C。归属和爱的需要 D。尊重的需要
- 借贷记账法的主要内容是什么?
- 当贷款的本金或利息逾期 90 天时,应单独核算。
- 下面哪个概念不属于社会学习理论( )。A.观察学习B.自我效能C.自我实现D.替代学习