电大经济数学基础12全套试题及答案汇总20220728.doc

设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。

A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解

答案：D

解析：

设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。

A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解

答案：D

解析：

设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。

A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解

答案：D

解析：

设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。

A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解

答案：D

解析：

设三次函数

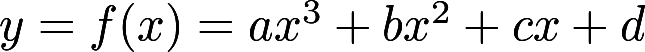, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是

A.关于y轴对称
B.关于原点对称
C.关于直线y=x轴对称
D.以上均错

答案：B

解析：

电大经济数学基础12全套试题及答案一、填空题(每题3分，共15分)6函数的定义域是7函数的间断点是8若，则9设，当0时，是对称矩阵。10若线性方程组有非零解，则1 。6函数的图形关于原点对称7已知，当0时，为无穷小量。8若，则9设矩阵可逆，B是A的逆矩阵，则当=。10若n元线性方程组满足，则该线性方程组有非零解。6函数的定义域是 7函数的间断点是。8若，则=9设，则 1。10设齐次线性方程组满，且，则方程组一般解中自由未知量的个数为3。6设，则=x2 47若函数在处连续，则k= 2。8若，则1/2F(2x-3) c9若A为n阶可逆矩阵，则 n 。10齐次线性方程组的系数矩阵经初等行变换化为，则此方程组的一般解中自由未知量的个数为2。1下列各函数对中，( D )中的两个函数相等2函数在处连续，则（ C1）。3下列定积分中积分值为0的是( A )4设，则( B. 2 ) 。5若线性方程组的增广矩阵为，则当=（ A1/2 ）时该线性方程组无解。6的定义域是 7设某商品的需求函数为，则需求弹性=。8若，则9当时，矩阵可逆。10已知齐次线性方程组中为矩阵，则。1函数的定义域是 2曲线在点（1,1）处的切线斜率是3函数的驻点是 14若存在且连续，则 .5微分方程的阶数为4 。1函数的定义域是 2 03已知需求函数，其中为价格，则需求弹性4若存在且连续，则 .5计算积分2。二、单项选择题(每题3分，本题共15分)1下列函数中为奇函数的是 ( C）A B C D2设需求量对价格的函数为，则需求弹性为（ D）。A BC D3下列无穷积分收敛的是 (B )A BC D4设为矩阵，为矩阵，则下列运算中（ A.）可以进行。A. B.C. D.5线性方程组解的情况是（ D无解）A有唯一解 B只有0解C有无穷多解 D无解1函数的定义域是 ( D）A B C D2下列函数在指定区间上单调增加的是（ B）。A BC D3下列定积分中积分值为0的是(A )A BC D4设为同阶可逆矩阵，则下列等式成立的是（ C.）。A. B.C. D.5若线性方程组的增广矩阵为，则当（ A）时线性方程组无解A B0 C1 D21下列函数中为偶函数的是( C）A B C D2设需求量对价格的函数为，则需求弹性为（ D）。A B C D3下列无穷积分中收敛的是(C )A B C D4设为矩阵，为矩阵，且乘积矩阵有意义，则为 ( B. ) 矩阵。A. B. C. D.5线性方程组的解的情况是（ A无解）A无解 B只有0解 C有唯一解 D有无穷多解1下列函数中为偶函数的是( C）A B C D2设需求量对价格的函数为，则需求弹性为（ A）。A B C D3下列函数中(B )是的原函数A B C D4设，则( C. 2 ) 。A. 0 B. 1 C. 2 D. 35线性方程组的解的情况是（ D有唯一解）A无解 B

设三次函数

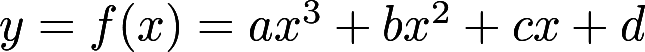, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是