二元函数z=x3-y3+3x2+3y2-9x的极小值点为( )A.(1,0)B.(1,2)C.(-3,0)D.(-3,2)
二元函数z=x3-y3+3x2+3y2-9x的极小值点为( )
A.(1,0)
B.(1,2)
C.(-3,0)
D.(-3,2)
B.(1,2)
C.(-3,0)
D.(-3,2)
参考解析
解析:【考情点拨】本题考查了二元函数的极值的知识点.【应试指导】
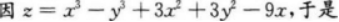

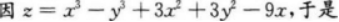

相关考题:
设函数f(x)在内连续,其导函数的图形如图所示,则f(x)有(52)。A.一个极小值点和两个极大值点B.两个极小值点和一个极大值点C.两个极小值点和两个极大值点D.三个极小值点和一个极大值点
f(x)在(-∞,+∞)内连续,其导数函数f′(x)图形如图所示,则f(x)有( )。A.一个极小值点和两个极大值点B.两个极小值点和两个极大值点C.两个极小值点和一个极大值点D.一个极小值点和三个极大值点
设函数y-f(x)连续,除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下,则y=f(x)A.有两个极大值点,一个极小值点,一个拐点B.有一个极大值点,一个极小值点,两个拐点C.有一个极大值点,一个极小值点,一个拐点D.有一个极大值点,两个极小值点,两个拐点
单选题设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )。A不是f(x,y)的连续点B不是f(x,y)的极值点C是f(x,y)的极大值点D是f(x,y)的极小值点