求由方程2x2+y2+z2+2xy-2x-2y-4x+4=0确定的隐函数的全微分.
求由方程2x2+y2+z2+2xy-2x-2y-4x+4=0确定的隐函数的全微分.
参考解析
解析: 所以dz=
所以dz=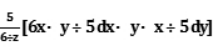
 所以dz=
所以dz=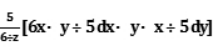
相关考题:
关于同步发电机机端三相短路的分析,下述说法中正确的是( )。A.派克变换的目的是将描述发电机电磁暂态过程的原始电压方程由变系数微分方程变为常系数微分方程B.将派克变换后的同步发电机基本方程进行拉普拉斯变换的目的是将基本方程由微分方程变为代数方程C.对同步发电机机端三相短路进行定量分析的基本方法是,利用象函数表示的发电机基本方程和边界条件,求出待求量的象函数,再进行拉普拉斯变换求待求量的原函数(d、q、0等效绕组系统中的电气量)D.派克变换仅适用于同步发电机三相对称短路的分析计算
设F(χ)=f(χ)g(χ),其中函数f(χ),g(χ)在(-∞,+∞)内满足以下条件: f’(χ)=g(χ),g’(χ)=f(χ),且f(0)=0,f(χ)+g(χ)=2eχ。 (1)求F(χ)所满足的一阶微分方程; (2)求出F(χ)的表达式。
关于同步发电机机端三相短路的分析,下述说法中错误的是:()。A、派克变换的目的是为了将描述发电机电磁暂态过程的原始电压方程由变系数微分方程变为常系数微分方程B、将派克变换后的同步发电机基本方程进行拉普拉斯变换的目的是将基本方程由微分方程变为代数方程C、对同步发电机机端三相短路进行定量分析的基本方法是,利用用象函数表示的发电机基本方程和边界条件,求出待求量的象函数,再进行拉普拉斯反变换求待求量的原函数(d、q、0等效绕组系统中的电气量),最后通过派克变换求出定子三相绕组系统中的电气量D、派克变换仅适用于同步发电机三相对称短路的分析计算
问答题设微分方程由通解y=(C1+C2x+x-1)e-x,求此微分方程。