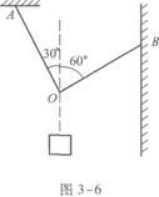
如图3-6所示,一根细绳的两端分别系于A点和B点,在0点处悬挂一个重物,质量m=10 kg,物体处于静止状态,则绳0B的张力是().(g取10 m/s2.)
如图3-6所示,一根细绳的两端分别系于A点和B点,在0点处悬挂一个重物,质量m=10 kg,物体处于静止状态,则绳0B的张力是().(g取10 m/s2.)

参考解析
解析:50 N【解题指要】本题考查的知识点是三个共点力的平衡问题.
先对物体m进行受力分析,m受两个作用力:竖直向下的重力G,竖直向上的绳子拉力F'.物体处于静止状态,所以G和F'是一对平衡力,根据平衡条件知.
F'=G=mg
再对O点作受力分析.O点处受到三个作用力:绳子OA的拉力FA,方向沿OA绳子向上;绳子OB的拉力FB,方向沿OB绳向上;下面绳子竖直向下的拉力F.图3-13是受力图.
由图知,FA、FB是相互垂直的.因此,在用力的平衡条件解题时,取OB方向为分解力的两个方向之一是最方便的.
根据力的平衡条件,FA、F在OB方向上分力之和等于FB.因为FA垂直于FB,它在OB方向上的分量为零,所以F在OB方向上的分力就等于FB.由此可知
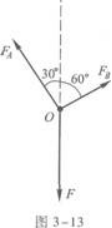
Fcos60°=FB
因此08绳子的张力为
FB=Fcos60°=F'cos60°=mgcos60°
代入题给数值得
FB=10×10×cos60°N=50 N
注意,在三个共点力平衡的问题中,通常可以取水平方向和竖直方向为分解力的两个方向.
根据力的平衡条件,沿水平方向有
FAsin30°=FB sin60°①
沿竖直方向有
FAcos30°+FBcos60°=F=mg②
由式①、②解得

显然,FA、FB的合力是F的平衡力-F,因为FA、FB相互垂直,所以由直角三角形的知识知FB=Fcos60°
先对物体m进行受力分析,m受两个作用力:竖直向下的重力G,竖直向上的绳子拉力F'.物体处于静止状态,所以G和F'是一对平衡力,根据平衡条件知.
F'=G=mg
再对O点作受力分析.O点处受到三个作用力:绳子OA的拉力FA,方向沿OA绳子向上;绳子OB的拉力FB,方向沿OB绳向上;下面绳子竖直向下的拉力F.图3-13是受力图.
由图知,FA、FB是相互垂直的.因此,在用力的平衡条件解题时,取OB方向为分解力的两个方向之一是最方便的.
根据力的平衡条件,FA、F在OB方向上分力之和等于FB.因为FA垂直于FB,它在OB方向上的分量为零,所以F在OB方向上的分力就等于FB.由此可知

Fcos60°=FB
因此08绳子的张力为
FB=Fcos60°=F'cos60°=mgcos60°
代入题给数值得
FB=10×10×cos60°N=50 N
注意,在三个共点力平衡的问题中,通常可以取水平方向和竖直方向为分解力的两个方向.
根据力的平衡条件,沿水平方向有
FAsin30°=FB sin60°①
沿竖直方向有
FAcos30°+FBcos60°=F=mg②
由式①、②解得

显然,FA、FB的合力是F的平衡力-F,因为FA、FB相互垂直,所以由直角三角形的知识知FB=Fcos60°
相关考题:
如图所示,实心物体A浸没在水中时,弹簧测力计示数为6N.将A制成空心体B(质量不变),放入装满水的溢水杯中,如图10乙所示,物体B处于悬浮状态,同时溢出水的质量为1kg.物体B空心部分的体积等于______m3.(g取10N/kg)
如图2-12所示,质量为4 kg的物体以5 m/s的速度冲上斜面.斜面的倾角为45°,物体与斜面间的摩擦因数μ=0.25.求:(取g=10m/s2)(1)物体能到达的最大高度;(2)物体克服摩擦力的功.
质量为10kg的物体,从20m.的高处自由落下,g取10m/s2.则第2秒末的即时功率是__________w,第2秒内的平均功率是__________W,2秒内的平均功率是__________W.
如图8-2所示,物块A放在水平的光滑桌面上,用细绳的一端系住A绳穿过小孔O,另一端系物块B.当A在桌面上以角速度ω=5 rad/s绕O做匀速圆周运动时,绳被拉紧,B静止才动.已知A的质量mA=1 kg,A离O的距离为1 m,则B的质量等于( )(取g=10 m/s2)A.2.5 kgB.2 kgC.1.5 kgD.0.5 kg
如图3-10所示,一个物体A从高为h的光滑坡面上下滑,滑到最低点时进入一辆停放在光滑水平面上的小车上,小车在A的带动下开始运动,最后A相对静止在小车上.已知:A的质量m1=2 kg,小车的质量m2=8 kg,A与车之间的摩擦因数μ=0.8,h=1.25 m.取g=10 m/s2,求:(1)A相对于小车静止时,小车速度的大小;(2)A相对于小车静止前,A在小车上运动的时间;(3)A在小车上滑行时,相对于地面运动的路程.
如图5—15所示,用一条细绳通过一个光滑的滑轮将一个0.20 kg的砝码和光滑桌面上的一个0.80 kg的小车连接在一起.开始时用手握住小车使砝码离开地面.1.0m,然后放手使小车从静止开始运动.试计算:(1)开始时砝码的重力势能(g取10 m/s2).(2)放手后砝码到达地面时小车的速度(桌面足够长).
如图所示,两物体M、N用绳子连接,绳子跨过固定在斜面顶端的滑轮(不计滑轮的质量和摩擦力),N悬于空中,M放在斜面上,均处于静止状态,当用水平向右的拉力F作用于物体M时,M、N仍静止不动,则下列说法正确的是( )。{图}A. 绳子的拉力始终不变B. M受到的摩擦力方向沿斜面向上C. 物体M所受到的合外力变大D. 物体M总共受到4个力的作用
如图.一不可伸长的光滑轻绳,其左端固定于0点,右端跨过位于O’点的固定光滑轴悬挂一质量为M的物体.00’,段水平,长度为L,绳子上套一可沿绳滑动的轻环。现在轻环上悬挂一钩码,平衡后物体上升L,则钩码的质量为( )。
如图所示,真空中有A、B两个等量异种点电荷,0、M、N是AB连线的垂线上的三个点,且A O>OB。一个带负电的检验电荷仅在电场力的作用下,从M点运动到N点,其轨迹如图中实线所示。若M、N两点的电势分别为M和N,检验电荷通过M、Ⅳ两点的动能分别为Ekm和Ekn,则( )。
如图所示,墙上有两点M和N分别钉有两铁钉,M和N的连线与水平方向的夹角为45。,两者的高度差为l。一条不可伸长的轻质细绳一端同定于M点的铁钉上,另一端跨过N点的光滑铁钉悬挂一质量为m1的重物,在绳上距M点l/2的P点系上一质量为m2的重物.平衡后绳的MP段正好水平。则m1/m2为( )。 A.51/2B.5/21/2C.2D.21/2
如图所示,一个内表面光滑的半球型碗放在水平桌面上,碗口处于水平状态,0是球心,有两个带同种电荷的质量分别为m1和m2的视为质点的小球,当它们静止后处于如图所示的状态,则m1和m2两球对碗的弹力大小之比为( )。
质量m1与半径r均相同的三个均质滑轮,在绳端作用有力或挂有重物,如图所示。已知均质滑轮的质量为m1=2kN·s^2/m,重物的质量分别为m2=2kN·s^2/m,m3=1kN·s^2/m,重力加速度按g=10m/s^2计算,则各轮转动的角加速度α间的关系是( )。 A. α1=α3>α2 B. α1<α2<α3 C. α1>α3>α2 D. α1≠α2=α3
质量为5.0×103kg的物体,在高空受到的重力为4.8104N,该处的重力加速度g=()m/s2。如果该处有另一质量为5kg的物体,放在竖直放置的劲度系数k=1000N/m的弹簧上,物体处于静止状态,则弹簧的压缩量x=()m。
用细绳悬挂在气球下面的物体以10m/s匀速上升,在离地面40m高度处细绳断开,绳断后物体不受任何阻力,g取10m/s²,则()A、物体立即做自由落体运动B、物体先向上做匀减速直线运动,再做自由落体运动C、物体离地的最大距离是40mD、物体离地的最大距离是45m
在轻质弹簧下端悬挂一质量为0.1kg的物体,当物体静止后,弹簧伸长了0.01m,取g=10m/s2。该弹簧的劲度系数为()A、1N/mB、10N/mC、100N/mD、1000N/m