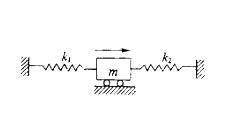
图示质量为m的物块,用两根弹性系数为k1和k2的弹簧连接,不计阻尼,当物体受到干扰力F=hsinωt的作用时,系统发生共振的受迫振动频率ω为:
图示质量为m的物块,用两根弹性系数为k1和k2的弹簧连接,不计阻尼,当物体受到干扰力F=hsinωt的作用时,系统发生共振的受迫振动频率ω为:
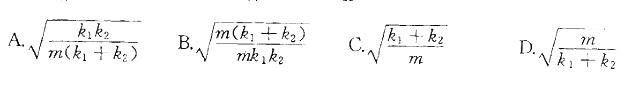

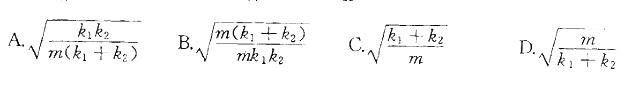
参考解析
解析:提示:当受迫振动频率与自由振动固有频率相等时,系统发生共振。(k1和k2为并联弹簧)
相关考题:
图示在倾角为α的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为:A. (k/m)1/2B.[k/(ms)]1/2C. [k/(msinα)]1/2D. (ksinα/m)1/2
在图示三个振动系统中,物块的质量均为m,弹賛的刚性系数均为k,摩擦和弹簧的质量不计。设图a)、b)、c)中弹簧的振动频率分别为f1、f2、f3,则三者的关系有:A.f1=f2≠f3B. f1≠f2=f3C. f1=f2=f3D. f1≠f2≠f3
一无阻尼弹簧-质量系统受简谐激振力作用,当激振频率为ω1=6rad/s时,系统发生共振。给质量块增加1kg的质量后重新试验,测得共振频率ω2=5.86rad/s。则原系统的质量及弹簧刚度系数是( )。 A.19.69kg,623.55N/mB.20.69kg,623.55N/mC.21.69kg,744.86N/mD.20.69kg,744.84N/m
图示一刚性系数为k的弹簧下挂一质量为m的物块,当物块处于平衡时弹簧的静伸长为δ,则当物块从静平衡位置下降距离h时,弹性力所做的功W为:A. W = 1/2k[(h + δ)2-δ2] B. W = 1/2k[δ2-(h + δ)2] C. W = 1/2k(δ +h )2 D. 1/2kh2
在图示三个振动系统中,物块的质量均为m,弹賛的刚性系数均为k,摩擦和弹簧的质量不计。设图a)、b)、c)中弹簧的振动频率分别为f1、f2、f3,则三者的关系有:A.f1=f2≠f3 B. f1≠f2=f3 C. f1=f2=f3 D. f1≠f2≠f3
一个10kg的质量支撑在弹性系数为1000N/m的弹簧上,其黏滞阻尼系数为5N﹒s/m,则临界阻尼比和系统的阻尼自然振动频率分别为()。A、0.025、0.8HzB、0.025、1.6HzC、0.050、0.8HzD、0.050、1.6Hz
符合受迫振动的特点的有()。A、受迫振动是指物体在受到策动力作用下所产生的振动B、其频率不依赖于策动力本身的频率C、其频率可以不同于振动系统的固有频率D、振幅达到最大时,策动力的频率等于振动物体的固有频率E、振幅达到最大时,发生共振现象
在弹性限度之内,一轻弹簧受到10N的拉力时,它的伸长量是4cm,则该弹簧劲度系数是()N/m,当弹簧不受拉力时,该弹簧劲度系数是()N/m,当弹簧两端受到拉力为10N时,弹簧的伸长量是()cm。
质量为5.0×103kg的物体,在高空受到的重力为4.8104N,该处的重力加速度g=()m/s2。如果该处有另一质量为5kg的物体,放在竖直放置的劲度系数k=1000N/m的弹簧上,物体处于静止状态,则弹簧的压缩量x=()m。
质量为2kg的物体放在水平地板上,用一轻弹簧水平拉该物体,当物体刚开始运动时,弹簧伸长了3cm,当拉着物体匀速前进时,弹簧伸长2cm,已知弹簧的劲度系数为k="200"N/m(g="10"N/kg),求: (1)物体所受的最大静摩擦力为多少? (2)物体和地板间的动摩擦因数。
单选题一个10kg的质量支撑在弹性系数为1000N/m的弹簧上,其黏滞阻尼系数为5N﹒s/m,则临界阻尼比和系统的阻尼自然振动频率分别为()。A0.025、0.8HzB0.025、1.6HzC0.050、0.8HzD0.050、1.6Hz