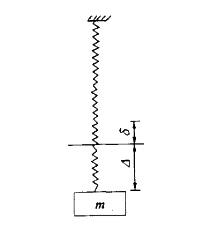
图示一弹簧常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降Δ距离,则弹性力所做的功为:
图示一弹簧常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降Δ距离,则弹性力所做的功为:



参考解析
解析:提示:直接采用用弹性力做功的公式。
相关考题:
在弹性限度内,弹簧伸长的长度与所挂物体的质量成正比。一根弹簧不挂物体时长15厘米;所挂物体质量为3千克时,弹簧长16.8厘米,求弹簧总长y(厘米)与所挂物体质量x的(千克)之间的函数关系式。
图示在倾角为α的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为:A. (k/m)1/2B.[k/(ms)]1/2C. [k/(msinα)]1/2D. (ksinα/m)1/2
匀质杆质量为m,长OA=l,在铅垂面内绕定轴O转动。杆质心C处连接刚度系数k较大的弹簧,弹簧另端固定。图示位置为弹簧原长,当杆由此位置逆时针方向转动时,杆上A点的速度为vA,若杆落至水平位置的角速度为零,则vA的大小应为:
图示一刚性系数为k的弹簧下挂一质量为m的物块,当物块处于平衡时弹簧的静伸长为δ,则当物块从静平衡位置下降距离h时,弹性力所做的功W为:A. W = 1/2k[(h + δ)2-δ2] B. W = 1/2k[δ2-(h + δ)2] C. W = 1/2k(δ +h )2 D. 1/2kh2
某弹簧的弹性系数为k,在I位置弹簧的变形为δ1,在II位置弹簧的变形为δ2。若取II位置为零势能位置,则在I位置弹性力的势能为:A.k(δ12-δ22) B.k(δ22-δ12) C.1/2k(δ12-δ22) D.1/2k(δ22-δ12)
质量为5.0×103kg的物体,在高空受到的重力为4.8104N,该处的重力加速度g=()m/s2。如果该处有另一质量为5kg的物体,放在竖直放置的劲度系数k=1000N/m的弹簧上,物体处于静止状态,则弹簧的压缩量x=()m。
实验室有甲、乙两种弹簧测力计,量程分别为5N和10N,它们的刻度总长度相同。用甲测量物体的重力,读数为4.20N,弹簧伸长了4.20cm。若用乙弹簧测量同一物体的重力时()A、两弹簧的劲度系数相同B、乙弹簧的读数为8.40NC、乙弹簧的伸长量为4.20cmD、乙弹簧受到的拉力为4.20N
一物体放到水平地板上,用一轻弹簧水平拉该物体,当物体刚开始运动时,弹簧伸长了3cm,当拉着物体匀速前进时,弹簧伸长了2cm,用弹簧测量此物体的重力时,弹簧伸长了10cm,己知弹簧的劲度系数为k=200N/m,(g=10N/kg)求: (1)物体所受的最大静摩擦力为多少? (2)物体和地板间的动摩擦因数。
劲度系数为k的轻弹簧,竖直放置,下端悬挂一质量为m的小球,使弹簧为原长而小球恰好与地面接触,今将弹簧上端缓缓地提高直到小球刚好离开地面为止,在此过程中,外力所做的功为()。A、m2g2/2k B、m2g2/k C、m2g2/4k D、4m2g2/k
质量为2kg的物体放在水平地板上,用一轻弹簧水平拉该物体,当物体刚开始运动时,弹簧伸长了3cm,当拉着物体匀速前进时,弹簧伸长2cm,已知弹簧的劲度系数为k="200"N/m(g="10"N/kg),求: (1)物体所受的最大静摩擦力为多少? (2)物体和地板间的动摩擦因数。