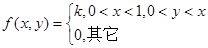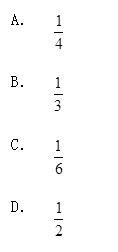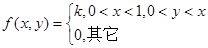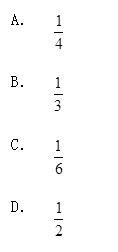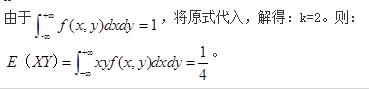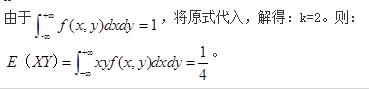二维连续性随机变量(X,Y)联合概率密度f(x,y)满足f(x,y)0。()
已知(X,Y)服从均匀分布,联合概率密度函数为设Z=max{X,Y}求Z的概率密度函数fz(z)
设X~U(0,2),y=X^2,求y的概率密度函数.
设随机变量X,y相互独立,且X~,Y~E(4),令U=X+2Y,求U的概率密度.
设随机变量(X,Y)的联合密度函数为f(x,y)=(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
设随机变量X的概率密度为fx(x)=求y=e^x的概率密度FY(y).
设随机变量X的概率密度函数为fxcx)=,则y=2X的密度函数为(y)=_______.
设二维随机变量(X,Y)的概率密度为则P{X+Y≤1}=_______.
设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2,与y=0所围成的三角形区域. (Ⅰ)求X的概率密度fx(x); (Ⅱ)求条件概率密度.
设随机变量X与Y独立,其中X的概率分布为而Y的概率密度为f(y),求随机变量U=X+Y的概率密度g(u).
设(X,Y)的联合概率密度为f(x,y)=求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.
设随机变量X在区间(0,1)内服从均匀分布,在X=x(0 (Ⅰ)随机变量X和Y的联合概率密度; (Ⅱ)Y的概率密度; (Ⅲ)概率P{X+Y>1}.
设随机变量X和Y的联合分布是正方形G={(x,y)|1≤x≤3,1≤y≤3}上的均匀分布,试求随机变量U=|X-Y|的概率密度p(u).
设二维随机变量(X,Y)的概率密度为 求常数A及条件概率密度.
设随机变量X的概率密度为令随机变量, (Ⅰ)求Y的分布函数; (Ⅱ)求概率P{X≤Y}.
设随机变量X,Y相互独立,且X的概率分布为P{X=0)=P{X=2)=,Y的概率密度为 (Ⅰ)求P{Y≤EY}; (Ⅱ)求Z=X+Y的概率密度.
设随机变量(X,Y)服从二维正态分布,其概率密度为f(x,y)=1/2π
设二维随机变量(X,Y)在区域D上服从均匀分布,其中D://0≤x≤2,0≤y≤2。记(X,Y)的概率密度为f(x,y),则f(1,1)=()
设随机变量X概率密度为p(x),Y=-X,则Y的密度为()。A、-p(y)B、1-p(-y)C、p(-y)D、.p(y)
设随机变量X的概率密度为fX(x),随机变量Y的概率密度为fY(y),则二维随机变量(X、Y)的联合概率密度为fX(x)fY(y)。
问答题37.设X~N(0,1),则Y=2X+1的概率密度fY(y)=
单选题设随机变量X的概率密度函数f(x)=1/[π(1+x2)],则Y=3X的概率密度函数为( )。A1/[π(1+y2)]B3/[π(9+y2)]C9/[π(9+y2)]D27/[π(9+y2)]
问答题设随机变景X与Y相互独立,且X服从[0,1]上的均匀分布,y服从λ=1的指数分布, 求:(1)X与Y的联合分布函数. (2)X与y的联合概率密度函数. (3)P{X≥Y}.
问答题设随机变量(X,Y)的概率密度为 求:(1)系数k. (2)边缘概率密度fX(x),fY(y). (3)P{X+Y1}.
问答题 随机变量(X,Y)在矩形区域D={(x,y)|a 求:(1)联合概率密度f(x,y). (2)边缘概率密度f X(i),f Y(y). (3)X与Y是否独立?
单选题设随机变量(X,Y)服从二维正态分布,且X与Y不相关,fX(x),fY(y)分别表示X,Y的概率密度,则在Y=y的条件下,X的条件概率密度fX|Y(x|y)为( )。AfX(x)BfY(y)CfX(x)fY(y)DfX(x)/fY(y)
问答题 设X与Y相互独立,X的概率密度为 Y的概率密度为 求:(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y),ρXY.