设随机变量X,Y相互独立,D(X)=4D(Y),令U=3X+2Y,V=3X-2Y,则=_______.

设随机变量X,Y相互独立,D(X)=4D(Y),令U=3X+2Y,V=3X-2Y,则=_______.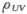

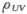参考解析

解析：Cov(U，V)=Cov(3X+2Y，3X-2Y)=9Cov(X，X)-4Cov(Y，Y)=9D(X)-4D(Y)=32D(Y)，由X，Y独立，得D(U)=D(3X+2Y)=9D(X)+4D(Y)=40D(Y)，D(V)=D(3X-2Y)=9D(X)+4D(Y)=40D(Y)，
所以

相关考题：

设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()
查看答案
设随机变量X,Y相互独立,X～U(0,2),Y～E(1),则.P(X+Y>1)等于().
查看答案
设随机变量X～U［0,2］,y=X^2,则X,Y().A.相关且相互独立B.不相互独立但不相关C.不相关且相互独立D.相关但不相互独立
查看答案
设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-YB.X+YC.X-2YD.Y-2X
查看答案
设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是( )。A.8B.16C.28D.44
查看答案
设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().
查看答案
设随机变量X,y相互独立,且X～,Y～E(4),令U=X+2Y,求U的概率密度.
查看答案
设随机变量X,Y,Z相互独立,且X～U［-1,3］,Y～B,Z～N(1,3……2),且随机变量U=X+2Y-32+2,则D(U)=_______.
查看答案
设X,Y为两个随机变量,D(X)=4,D(Y)=9,相关系数为,则D(3X-2Y)=_______.
查看答案
设随机变量X~U（0，1)，Y~E（1），且X,Y相互独立，求Z=X+Y的密度函数
查看答案
设随机变量X～U(0,1),Y～E(1),且X,Y相互独立,求随机变量Z=X+Y的概率密度.
查看答案
设随机变量X和Y相互独立,且分布函数为Fx(x)=,Fy(y)=,令U=X+Y,则U的分布函数为_______.
查看答案
设随机变量X～N(μ,σ^2),Y～U［－π,π］,X,Y相互独立,令Z=X+Y,求fz(z).
查看答案
设随机变量X,Y相互独立且都服从标准正态分布,令U=X^2+Y^2.求：　　(1）(u);(2)P{U>D(U)｜U>E(U)}.
查看答案
设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y～.则P(X-1-2Y≤4)=_______.
查看答案
设X,Y相互独立,且X～B,Y～N(0,1),令U=max{X,Y},求P{1
查看答案
设随机变量(X,Y)在区域D={(z,y)｜0≤x≤2,0≤y≤1}上服从均匀分布,令　　U=,V=.　　(1)求(U,V)的联合分布；(2)求.
查看答案
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.　　设随机变量U=max{X,Y},V=min{X,Y}.　　(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；　　(3)判断U,V是否相互独立？(4)求P（U=V）.
查看答案
设随机变量X与Y相互独立，且EX与EY存在，记U=max{X，Y}，V=min{X，Y}，则E(UV)= A.AEU·EVB.EX·EYC.EU·EYD.EX·EV
查看答案
设随机变量X和Y独立同分布，记U＝X－Y，V＝X+Y，则随机变量U与V也（ ）。《》（ ）A.不独立；B.独立；C.相关系数不为零；D.相关系数为零。
查看答案
随机变量X与Y相互独立，且D（X）=4，D（Y）=2，则D（3X－2Y）＝（）。
查看答案
设随机变量X、Y相互独立，且D（X）=1，D（Y）=2，则D（3X-2Y）=（）。
查看答案
设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。
查看答案
设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是（）A、8B、16C、28D、44
查看答案
设随机变量X与Y相互独立，X~π（2），Y~π（3），则P{X+Y≤1}=（）。
查看答案
多选题数学期望的性质包括（）A设c为常数，则E（c）＝cB设X为随机变量，α为常数，则E（αX）＝αE（X）C设X、y是两个随机变量，则E（X±Y）＝E（X）＋E（Y）D设X、y是相互独立的随机变量，则E（XY）＝E（X）E（Y）E设c为常数，则E（c）＝0。
查看答案
单选题设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是（　　）。A8B16C28D44
查看答案
热门标签