某种电子元件的重量x(单位:g)服从正态分布,μ,σ2均未知。测得16只元件的重量如下:159,280,101,212,224,379,179,264,222,362,168,250,149,260, 485,170,判断元件的平均重量是否大于225g(取α=0.05)。下列计算过程中正确的提法有( )。A.提出假设:H0:μ≤225;H1:μ>225B.提出假设:H0:μ≥225;H1:μ<225C.检验统计量及其概率分布为D.取α=0.05,经计算有:T<t0.05(15)E.接受H0,即认为元件的平均重量不大于225g
某种电子元件的重量x(单位:g)服从正态分布,μ,σ2均未知。测得16只元件的重量如下:159,280,101,212,224,379,179,264,222,362,168,250,149,260, 485,170,判断元件的平均重量是否大于225g(取α=0.05)。下列计算过程中正确的提法有( )。
A.提出假设:H0:μ≤225;H1:μ>225
B.提出假设:H0:μ≥225;H1:μ<225
C.检验统计量及其概率分布为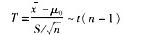
D.取α=0.05,经计算有:T<t0.05(15)
E.接受H0,即认为元件的平均重量不大于225g
相关考题:
设X服从均数为μ,标准差为σ的正态分布,通过μxΓ/ξ的标准化变换,则A.转换后变量的均数不变而标准差改变,且服从正态分布B.转换后变量的均数改变而标准差不变,且服从正态分布C.转换后变量的均数和标准差都改变,且服从正态分布D.转换后变量的均数和标准差都不变,但不服从正态分布E.转换后变量的均数和标准差都不变,且服从正态分布
某糖厂生产袋糖,已知袋糖重量服从正态分布,规定平均重量不低于500g,今从一批袋糖中随机抽取12袋,测得=510g,s=18g。检验袋糖平均重量是否符合规定的原假设H0为( )。A.μ=500B.μ≥500C.μ≤500D.μ≠500
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差口为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平α=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。A.提出假设H0:μ≤100;H1:μ>100B.提出假设H0:μ≥100;H1:μ<100C.检验统计量及所服从的概率分布为D.如果Z>Zα,则称与μ0的差异是显著的,这时拒绝H0E.检验结果认为该类型的电子元件的使用寿命确实有显著提高
某糖果厂用自动包装机装糖,每包重量服从正态分布,某日开工后随机抽查10包的重量如下:494,495,503,506,492,493,498,507,502,490(单位:克)。已知σ=5,显著性水平为0.05。根据上述资料请回答:求总体均值的置信区间时,先构造统计量是( )。
某药片重量(毫克)服从正态分布,现知该药片100片的平均重量服从正态分布N (20,0. 152),则该药单片重量的分布是( )。A.N (20,0.152) B. N (20,0.0152)C.N (20,152) D. N (20, 1. 52)
某商场从~批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。根据上述资料请答:选择的检验统计量是()。查看材料
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差a为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平a=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。
某商场从~批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。根据上述资料请答:假设检验的拒绝域是()。查看材料
某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。 选择的检验统计量是()。
某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789.780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。根据上述资料请回答:假设检验的拒绝域是()。A.(- ∞,-zα/2]∪[zα/2, +∞)B.(- ∞,-tα/2]∪[tα/2, +∞), tα/2= tα/2(n)C.(- ∞,-tα/2]∪[tα/2, +∞), tα/2= tα/2(n-1)D.( tα,+∞)
某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。据此回答以下四题83-86。 提出原假设与各择假设为( )。
设X服从均数为μ、标准差为σ的正态分布,作u=(X-μ)/σ的变量变换,则()。A、u服从正态分布,且均数不变B、u服从正态分布,且标准差不变C、u服从正态分布,且均数和标准差都不变D、u服从正态分布,但均数和标准差都改变E、u不服从正态分布
设某种电灯泡的寿命X服从正态分布N(μ,σ2),其中是未知的,现在随机的抽取4只这种灯泡,测得其寿命为1500,1455,1368,1649,是估计总体均值为()A、1500B、1649C、1493D、1368
问答题40.已知某种类型电子元件的寿命X(单位:小时)服从指数分布,它的概率密度为 一台仪器装有4个此种类型的电子元件,其中任意一个损坏时仪器便不能正常工作.假设4个电子元件损坏与否互相独立. 试求:(1)一个此种类型电子元件能工作2 000小时以上的概率p1; (2)一台仪器能正常工作2 000小时以上的概率p2.
单选题设某种电灯泡的寿命X服从正态分布N(μ,σ2),其中是未知的,现在随机的抽取4只这种灯泡,测得其寿命为1500,1455,1368,1649,是估计总体均值为()A1500B1649C1493D1368
不定项题某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。 请根据上述资料请回答下列问题。提出原假设与备择假设为( )。ABCD
问答题从某种型号的晶体管中抽取10件做样本测量其寿命,测得寿命的标准差为s=45(小时),设这批晶体管的寿命服从于正态分布N(μ,σ2),其中μ,σ2均为未知,求σ2的置信度为0.975的单侧置信上限。
不定项题某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。 请根据上述资料请回答下列问题。选择的检验统计量是( )。ABCD
不定项题某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。 请根据上述资料请回答下列问题。 假设检验的拒绝域是( )。ABCD