某药片重量(毫克)服从正态分布,现知该药片100片的平均重量服从正态分布N (20,0. 152),则该药单片重量的分布是( )。A.N (20,0.152) B. N (20,0.0152)C.N (20,152) D. N (20, 1. 52)
某药片重量(毫克)服从正态分布,现知该药片100片的平均重量服从正态分布N (20,0. 152),则该药单片重量的分布是( )。
A.N (20,0.152) B. N (20,0.0152)
C.N (20,152) D. N (20, 1. 52)
A.N (20,0.152) B. N (20,0.0152)
C.N (20,152) D. N (20, 1. 52)
参考解析
解析: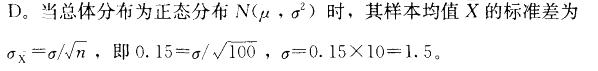
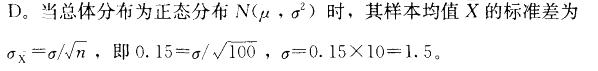
相关考题:
某糖厂生产袋糖,已知袋糖重量服从正态分布,规定平均重量不低于500g,今从一批袋糖中随机抽取12袋,测得=510g,s=18g。检验袋糖平均重量是否符合规定的原假设H0为( )。A.μ=500B.μ≥500C.μ≤500D.μ≠500
设Xi(i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi(i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi(i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b]上的均匀分布,则服从正态分布D.无论Xi(i=1,2,…,n)服从何种相同的分布,其均值都服从正态分布
设Xi (i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi (i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi (i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b)上的均匀分布,则服从正态分布D.无论Xi (i=1,2,…,n)服从何种分布,其均值都服从正态分布
关于中心极限定理,下列说法正确的是( )。A.多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布B. n个相互独立同分布随机变量,其共同分布不为正态分布或未知,但其均值μ和方差σ2都存在,则在n相当大的情况下,样本均值近似服从正态分布N(μ, σ2/n)C.无论什么分布(离散分布或连续分布,正态分布或非正态分布),其样本均值的分布总近似于正态分布D.设n个分布一样的随机变量,假如其共同分布为正态分布N(μ, σ2)则样本均值仍为正态分布,其均值不变仍为μ,方差为 σ2/n
某商场从~批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。根据上述资料请答:选择的检验统计量是()。查看材料
某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789,780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。 选择的检验统计量是()。
下面几个关于样本均值分布的陈述中,正确的是( )。Ⅰ.当总体服从正态分布时,样本均值一定服从正态分布Ⅱ.当总体服从正态分布时,只要样本容量足够大,样本均值就服从正态分布Ⅲ.当总体不服从正态分布时,样本均值一定服从正态分布Ⅳ.当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布Ⅴ.当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布 A、Ⅰ.ⅤB、Ⅰ.Ⅱ.Ⅲ.ⅣC、Ⅰ.Ⅱ.ⅣD、Ⅱ.Ⅲ.Ⅳ
设X服从均数为μ、标准差为σ的正态分布,作u=(X-μ)/σ的变量变换,则()。A、u服从正态分布,且均数不变B、u服从正态分布,且标准差不变C、u服从正态分布,且均数和标准差都不变D、u服从正态分布,但均数和标准差都改变E、u不服从正态分布
多选题抽样分布中()。A如果总体服从正态分布,则样本均值也服从正态分布B如果总体不服从正态分布,则样本均值也不服从正态分布C在大样本的情况下,即使总体不服从正态分布,样本均值也服从正态分布D如果总体服从正态分布,则样本均值不一定服从正态分布E如果总体不服从正态分布,样本均值不一定不服从正态分布
判断题如果总体服从正态分布,则样本均值也服从正态分布;如果总体不服从正态分布,则样本均值也不服从正态分布。()A对B错