曲线x=t2/2,y=t+3,z=(1/18)t3+4 (t≥0)上对应于面的夹角为:A.π/3 B.π/6 C.π/2 D.π/4
曲线x=t2/2,y=t+3,z=(1/18)t3+4 (t≥0)上对应于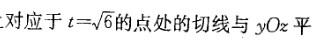
面的夹角为:
A.π/3 B.π/6 C.π/2 D.π/4
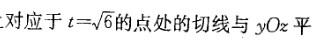
面的夹角为:
A.π/3 B.π/6 C.π/2 D.π/4
参考解析
解析:提示:利用向量和平面的夹角的计算公式计算。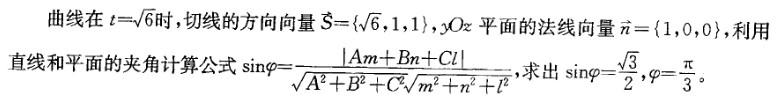
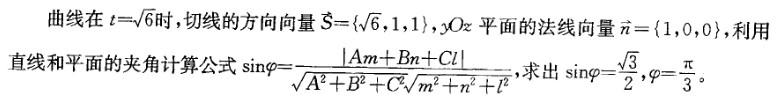
相关考题:
【说明】现有一个事务集{T1,T2,T3,T4),其中这四个事务在运行过程中需要读写X、Y和Z。设Ti对X的读操作记作TiR(X),Ti对X的写操作记作Tiw(X)。事务对XYZ的访问情况如下:T1: T1R(X)T2: T2R(Y),T2w(X)T3: T3w(Y),T3w(X),T3w(Z)T4: T4R(Z),T4w(X)试述事务并发高度的正确性准则及其内容。
下面程序的输出结果是()。includevoid main(){int x=-1,y=5,z;z=(x++ 下面程序的输出结果是( )。#include<iostream.h>void main(){int x=-1,y=5,z;z=(x++<0) (y-->=0);cout<<x<<'\t'<<y<<'\t'<<z<<end1;}A.-1 5 0B.-1 4 1C.0 4 1D.0 4 0
以下程序的输出结果为:public class test {public static void main(String args[]) {int x=1,y=1,z=1;if (x--==1}} A. x=0,y=2,z=1B. x=1,y=2,z=1C. x=0,y=1,z=1D. x=0,y=2,z=2
过点(1,0,0),(0,1,0),且与曲面z=x^2+y^2相切的平面为 A.Az=0与x+y-z=1B.z=0与2x+2y-z=2C.x=y与x+y-z=1D.x=y与2x+2y-z=2
在曲线x=t,y=t2,z=t3上某点的切线平行于平面x+2y+z=4,则该点的坐标为:()A、(-1/3,1/9,-1/27),(-1,1,-1)B、(-1/3,1/9,-1/27),(1,1,1)C、(1/3,1/9,1/27),(1,1,1)D、(1/3,1/9,1/27),(-1,1,-1)
单选题设平面α平行于两直线x/2=y/(-2)=z及2x=y=z,且与曲面z=x2+y2+1相切,则α的方程为( )。A4x+2y-z=0B4x-2y+z+3=0C16x+8y-16z+11=0D16x-8y+8z-1=0
单选题在曲线x=t,y=t2,z=t3上某点的切线平行于平面x+2y+z=4,则该点的坐标为:()A(-1/3,1/9,-1/27),(-1,1,-1)B(-1/3,1/9,-1/27),(1,1,1)C(1/3,1/9,1/27),(1,1,1)D(1/3,1/9,1/27),(-1,1,-1)