矩阵与相似的充分必要条件为( )A.a=0,b=2B.a=0,b为任意常数C.a=2,b=0D.a=2,b为任意常数
矩阵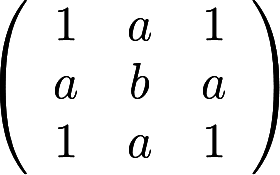 与
与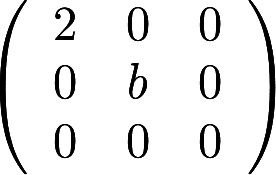 相似的充分必要条件为( )
相似的充分必要条件为( )
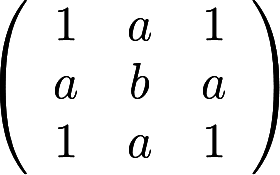 与
与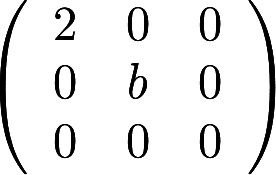 相似的充分必要条件为( )
相似的充分必要条件为( )A.a=0,b=2
B.a=0,b为任意常数
C.a=2,b=0
D.a=2,b为任意常数
B.a=0,b为任意常数
C.a=2,b=0
D.a=2,b为任意常数
参考解析
解析:

相关考题:
相似第三定理是:如果相似指标为1或相似判据相等且其它单值条件(边界条件、初始条件等)相同,则两现象必相似。相似第三定理是相似的()。 A、必要条件B、充分条件C、判据存在定理D、充分必要条件
设A是n阶矩阵,下列结论正确的是().A.A,=B都不可逆的充分必要条件是AB不可逆B.r(A)}C.AX==与BX=0同解的充分必要条件是r(A)=r(B)D.A~B的充分必要条件是λE-A~λE-B
单选题设向量组Ⅰ:α(→)1,α(→)2,…,α(→)m,其秩为r;向量组Ⅱ:α(→)1,α(→)2,…, α(→)m,β(→),其秩为s,则r=s是向量组Ⅰ与向量组Ⅱ等价的( )。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件
单选题设向量组I:α(→)1,α(→)2,…,α(→)m,其秩为r;向量组II:α(→)1,α(→)2,…,α(→)m,β(→),其秩为s,则r=s是向量组I与向量组II等价的( )。A充分非必要条件B必要非充分条件C充分必要条件D既非充分也非必要条件