设随机变量X服从指数分布，其概率密度为 ，则有( )。A、E(X)=θ，D(X)=θ2B、E(X)=θ2，D(X)=θC、E(X)=0，D(X)=θD、E(X)=0，D(X)=θ2
设随机变量X服从指数分布，其概率密度为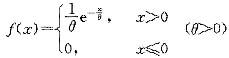 
，则有( )。
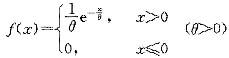，则有( )。A、E(X)=θ，D(X)=θ2
B、E(X)=θ2，D(X)=θ
C、E(X)=0，D(X)=θ
D、E(X)=0，D(X)=θ2
B、E(X)=θ2，D(X)=θ
C、E(X)=0，D(X)=θ
D、E(X)=0，D(X)=θ2
参考解析
解析：要记住重要的随机变量的数学期望E(X)和D(X)，对指数分布E(X)=θ，D(X)=θ2
相关考题：
设随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为P{Y=-1}=p，P{Y=1)=1-p，(0 (Ⅰ)求Z的概率密度； (Ⅱ)p为何值时，X与Z不相关； (Ⅲ)X与Z是否相互独立？
问答题15.设随机变量X的概率密度为