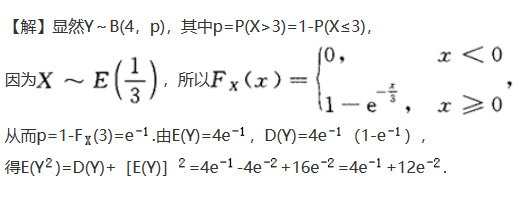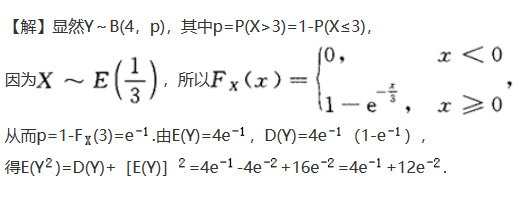已知总体X服从参数为λ的指数分布,设X1,X2,…,Xn是子样观察值,求λ的极大似然估计。
设随机变量X与Y相互独立.已知X服从区间(1，5)上的均匀分布，Y服从参数λ=5的指数分布，则D(3X-5Y)等于( ).A.5B.9C.10D.13
设随机变量X与Y相互独立且都服从参数为A的指数分布,则下列随机变量中服从参数为2λ的指数分布的是().A.X+yB.X-YC.max{X,Y}D.min{X,Y}
设随机变量X的概率密度为则Y表示对X的3次独立重复观察中事件{x=1/2}出现的次数，则P{Y=2}=:A.3/64 B.9/64 C.3/16 D.9/16
设随机变量X的概率密度为 对X独立地重复观察4次，用Y表示观察值大于的次数，求Y^2的数学期望.
随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为令Z=XY。p为何值时，X与Z不相关
设X～f(x)=对X进行独立重复观察4次,用Y表示观察值大于的次数,求E(Y^2).
设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.
设随机变量X服从参数为2的指数分布,证明：Y=1-在区间(0,1)上服从均匀分布.
随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为。求Z的概率密度
设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X
设随机变量X的概率密度为 对X进行独立重复的观测，直到第2个大于3的观测值出现时停止，记Y为观测次数. (Ⅰ)求Y的概率分布； (Ⅱ)求EY.
设随机变量Y服从参数为1的指数分布，a为常数且大于零，则P{Y≤a+1｜Y>a}=________.
设随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为P{Y=-1}=p，P{Y=1)=1-p，(0 (Ⅰ)求Z的概率密度； (Ⅱ)p为何值时，X与Z不相关； (Ⅲ)X与Z是否相互独立？
若随机变量X与Y相互独立，且X在区间[0,2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E(XY)等于：
设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。
设随机变量X的概率密度为，用Y表示对X的3次独立重复观察中事件出现的次数，则P{Y=2}=( )。A.3/64 B.9/64 C.3/16 D. 9/16
设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。A、1B、3
设随机变量Y服从参数为1的指数分布，a为常数且大于零，则P{Y≤a+1|Ya}=（）
设随机变量X服从参数为2的泊松分布，且Y=3X-2，则E（Y）=（）。
设随机变量X与Y相互独立，已知X服从区间（1，5）上的均匀分布，Y服从参数λ=5的指数分布，则D（3X-5Y）等于（）．A、5B、9C、10D、13
设随机变量X，Y相互独立，其中X在[0，6]上服从均匀分布，Y服从参数为λ=3的泊松分布，记Z=X-2Y，则D（Z）=（）。
设随机变量X服从参数为2的泊松分布，且Y=3X-2，求E（Y）。
设随机变量X服从参数为2，p的二项分布，随机变量Y服从参数为3，p的二项分布，若P{X≥1}=5/9，则P{Y≥1}=（）。
问答题X服从参数为2的指数分布，Y服从参数为4的指数分布，则E(2X2+3Y)=____ .
单选题设随机变量X与Y相互独立，已知X服从区间（1，5）上的均匀分布，Y服从参数λ=5的指数分布，则D（3X-5Y）等于（）．A5B9C10D13
单选题设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。A1B3
的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).