对回归方程线性关系的显著性进行检验。其检验过程应包括( )。A．提出假设：原假设H0：β1=β2=…=βk=0；备择假设H1：β1，β2：，…，βk不全为零B．构造的统计量为：样本统计量服从自由度为(k，n-k-1)的F分布C．根据给定的显著性水平，确定临界值Fα(k，n-k-1)D．如果F＞Fα(k，n-k-1)，则拒绝原假设E．如果F＞Fα(k，n-k-1)，表明在(1-α)的置信概率下，模型的线性关系显著成立，模型通过方程显著性检验
对回归方程线性关系的显著性进行检验。其检验过程应包括( )。
A．提出假设：原假设H0：β1=β2=…=βk=0；备择假设H1：β1，β2：，…，βk不全为零
B．构造的统计量为：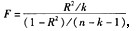
样本统计量服从自由度为(k，n-k-1)的F分布
C．根据给定的显著性水平，确定临界值Fα(k，n-k-1)
D．如果F＞Fα(k，n-k-1)，则拒绝原假设
E．如果F＞Fα(k，n-k-1)，表明在(1-α)的置信概率下，模型的线性关系显著成立，模型通过方程显著性检验
相关考题：
对回归方程线性关系显著性的检验中，显著性水平α是（ ）。A．原假设H为正确时被拒绝的概率 0B．原假设H0为正确时被接受的概率C．原假设H0为不正确时，被拒绝的概率D．原假设H为不正确时，被接受的概率
检验回归系数和回归方程的线性关系是否显著，正确的说法是( )。A．F检验用来检验回归系数的显著性，其假设为H0:β1=0；H0:β1≠0B．F检验用来检验回归方程线性关系是否显著，其假设为：H0：回归方程线性关系不显著；H1：回归方程线性关系显著C．t检验用来检验回归系数的显著性，其假设为H0:β1=0；H0:β1≠0D．t检验用来检验回归方程线性关系是否显著，其假设为：H0回归方程线性关系不显著；H1：回归方程线性关系显著
根据样本观测值和估计值计算t统计量，其值为t=50.945，根据显著性水平（）与自由度，由t分布表查得t分布的右侧临界值为2.365，所以（ ）。 05.0=aA．拒绝原假设，接受备择假设B．拒绝备择假设，接受原假设C．表明在95%的置信概率下，不是由=0这样的总体产生的 1?β1βD．在95%的置信概率下，人均可支配收入对人均消费性支出的影响是显著的
根据样本观测值和估计值计算t统计量，其值为t=12.660，根据显著性水平(a=0.05)与自由度，由t分布表查得分布的右侧临界值为2.571，所以( )。A．拒绝原假设，接受备择假设B．拒绝备择假设，接受原假设C．表明在95%的置信概率下，不是由β1=0这样的总体产生的D．在95%的置信概率下，该企业的产量对利润的影响是显著的
对该企业的工资总额趋势模型进行检验，得到方差分析计算结果F=634.65，则以下正确的是 ( )。A．该检验的假设为：H0:β1=0，H1:β1≠0B．该检验的假设为：H0:β1＜0，H1:β1≥0C．给定显著性水平α，查F分布表得到临界Fα(1，n-2)。这里F＞Fα(1,n-2)，所以拒绝原假设。D．给定显著性水平α，查F分布表得到临界Fα/2(1，n-2)。这里F＞Fα/2(1,n-2)，所以拒绝原假设。
对回归方程线性关系显著性的检验中，显著性水平。是( )。A．原假设H0为正确时被拒绝的概率B．原假设H0为正确时被接受的概率C．原假设H0为不正确时，被拒绝的概率D．原假设H0为不正确时，被接受的概率
进行回归方程线性关系的显著性检验时，根据样本资料计算的统计量值F=83.291，由于F＞F0.05,2,12，故( )。A．落入接受域，接受原假设B．落入拒绝域，接受备择假设C．在95%的置信概率下，模型的线性关系显著成立D．在95%的置信概率下，月工作时间和月完成任务量在整体上对月工资收入的解释作用是显著的
在假设检验中，下面的说法正确的是( )。A．建立假设时，有原假设H0和备择假设H1B．已知μ0，可假设H0:μ=μ0，H1:μ≠μ0检验样本均值是否为μ0C．正态总体σ己知时，μ的显著性水平为α的检验采用作为检验统计量D．假设H0:μ≤μ0，H1:μ＞μ0，是双侧假设检验E．假设H0:μ=μ0，H1:μ≠μ0，是双侧假设检验
假设检验的程序包括（ ）。①根据实际问题，提出原假设及备择假设②构造统计量并找出在假设成立条件下，该统计量所服从的概率分布③根据给定显著性水平和所选取的统计量，查概率分布临界值表，确定临界值与否定域④检验样本统计量的值是否落入否定域，若是则拒绝原假设，否则接受原假设A.①②④B.①③④C.②③④D.①②③④
假设检验的具体步骤包括（ ）。Ⅰ根据实际问题的要求，提出原假设及备择假设Ⅱ确定检验统计量，并找出在假设成立条件下，该统计量所服从的概率分布Ⅲ根据所要求的显著性水平和所选取的统计量，查概率分布临界值表，确定临界值与否定域Ⅳ判断计算出的统计量的值是否落入否定域，如落人否定域，则拒绝原假设；否则接受原假设A、Ⅰ、Ⅱ、ⅢB、Ⅰ、Ⅱ、ⅣC、Ⅰ、Ⅲ、ⅣD、Ⅰ、Ⅱ、Ⅲ、Ⅳ
下面关于单侧和双侧假设检验的说法，正确的有（ ）。A.在显著性水平a下，检验假设H0：μ=μ0；H1：μ≠μ0。的假设检验，称为双侧假设检验B.右侧检验和左侧检验统称为单侧检验C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μD.在显著性水平a下，检验假设H0：μ≥μ0；H1：μE.在显著性水平a下，检验假设H0：H0≤μ0；H1：μ>μ0的假设检验，称为右侧检验
下面关于单侧和双侧假设检验的说法，正确的有（）。A.在显著性水平a下，检验假设H0：μ=μ0；H1：μ≠μ0的假设检验，称为双侧假设检验B.右侧检验和左侧检验统称为单侧检验C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μD.在显著性水平a下，检验假设H0：μ>／μ0；H1：μE.在显著性水平a下，检验假设H0：μ=μ0；H1：μ>μ0的假设检验，称为右侧检验
下面关于单侧和双侧假设检验的说法，正确的有()。A.在显著性水平α下，检验假设风：H0:μ=μ0; H1:μB.右侧检验和左侧检验统称为单侧检验C.在显著性水平α下，检验假设H0:μ1 ≥μ0; H1:μD.在显著性水平α下，检验假设H0:μ1 ≥μ0; H1:μE.在显著性水平α下，检验假设H0:μ1 ≤μ0; H1:μ>μ0的假设检验，称为右侧检验
异质性检验的统计量服从何种分布(k为研究的个数n为第i个研究的样本量)：A.自由度为∑n-k的卡方分布B.自由度为k-1的卡方分布C.自由度为k-1的F分布D.自由度为∑n-k的F分布E.自由度为k-1的t分布
下列属于假设检验的一般步骤的有（ ）。Ⅰ.根据实际问题的要求,充分考虑和利用已知的背景知识,提出原假设H0及备择假设H1Ⅱ.给定显著性水平α以及样本容量nⅢ.确定检验统计量U,并在原假设H0成立的前提下导出U的概率分布,要求U的分布不依赖于任何未知参数Ⅳ.确定拒绝域A.Ⅱ.Ⅲ.ⅣB.Ⅰ.Ⅲ.ⅣC.Ⅰ.Ⅱ.ⅣD.Ⅰ.Ⅱ.Ⅲ.Ⅳ
在给定的显著性水平下，进行假设检验，确定拒绝域的依据是（）。A、原假设为真的条件下检验统计量的概率分布B、备择假设为真的条件下检验统计量的概率分布C、原假设为真的条件下总体参数的概率分布D、备择假设为真的条件下总体参数的概率分布
单选题回归系数βi在1－α的置信水平下的置信区间为（ ）。Aβ(∧)i±tα（n－k－1）s（β(∧)i）Bβ(∧)i±tα/2（n－k－1）s（β(∧)i）Cβ(∧)i±tα（n－k）s（β(∧)i）Dβ(∧)i±tα/2（n－k）s（β(∧)i）
单选题进行假设检验时，对于原假设H0和备择假设H1，检验概率值P-值（）。A是H0为真的概率值B是H1为真的概率值C是H0为假的概率值D如果小于或等于显著性水平 ，就拒绝H0