设函数f(x)=cos2x+2asinx-a(x∈R,a∈R)的最大值是2,求a的值。
设函数f(x)=cos2x+2asinx-a(x∈R,a∈R)的最大值是2,求a的值。
参考解析
解析: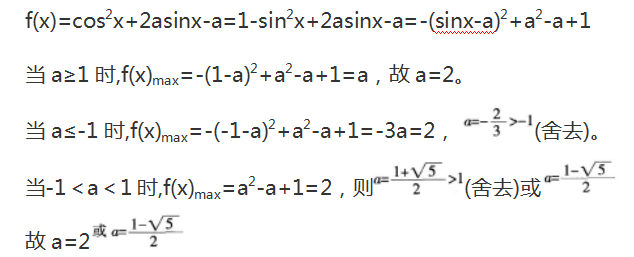
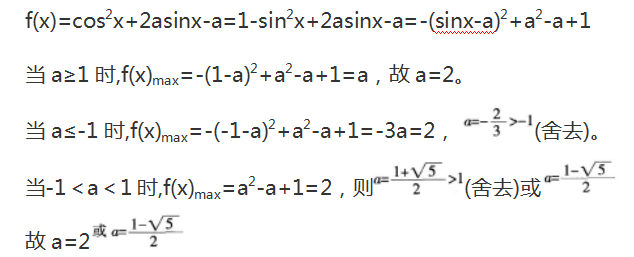
相关考题:
设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3:f1:R→R,f(x)=2xf2:N→N×N,f(n)=f 设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3: f1:R→R,f(x)=2x f2:N→N×N,f(n)=<n,n+1> f3:N→N,f(x)=x mod 3,x除以3的余数 则下面说法正确的是( )。A.f1和f2是单射但不是满射函数B.f1和f3都是满射函数C.f2是双射函数D.以上说法全都是错误的
设R,N分别表示实数、整数和自然数集,下面定义函数f1,f2,f3: fl:R→R,f(x)=2x f2:N→N×N,f(n)=<n,n+1> f3:N→N,f(x)=x mod 3,x除以3的余数 则下面说法正确的是A.n和f2是单射但不是满射函数B.f1和f3都是满射函数C.f2是双射函数D.以上说法全都是错误的
设函数findbig已定义为求3个数中的最大值。以下程序将利用函数指针调用findbig函数,请填空。main(){ int findbig(int,int,int); int (*f)(),x,y,z,big; f=; scanf("%d%d%d",x,y,z); big=(*f)(x,y,z); printf("big=%d\n",big);}
设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。A.f(0)是f(x)在(-a,a)的极大值,但不是最大值B.f(0)是f(x)在(-a,a)的最小值C.f(0)是f(x)在(-a,a)的极大值,也是最大值D.f(0)是曲线y=f(x)的拐点的纵坐标
设f(x)在(-a,a)是连续的偶函数,且当0A. f(0)是f(x)在(-a,a)的极大值,但不是最大值B. f(0)是f(x)在(-a,a)的最小值C. f(0)是f(x)在(-a,a)的极大值,也是最大值D. f(0)是曲线y=f(x)的拐点的纵坐标
设f(x)在(-a,a)是连续的偶函数,且当0()A、f(0)是f(x)在(-a,A.的极大值,但不是最大值B、B.f(0)是f(x)在(-a,的最小值C、C.f(0)足f(x)在(-a,的极大值,也是最大值D、f(0)是曲线y=f(x)的拐点的纵坐标
单选题设f(x)是R上的函数,则下列叙述正确的是()。Af(x)f(-x)是奇函数Bf(x)|f(x)|是奇函数Cf(x)-f(-x)是偶函数Df(x)+f(-x)是偶函数