已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。 该企业现有资本存量为当面临短期的产品价格波动时,它将如何生产?
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。 该企业现有资本存量为

当面临短期的产品价格波动时,它将如何生产?

当面临短期的产品价格波动时,它将如何生产?
参考解析
解析:对于该企业而言,利润函数为:π=PQ-vK-ωL 在短期,当资本存量一定时,厂商的利润函数为:

企业利润最大化的一阶条件为:
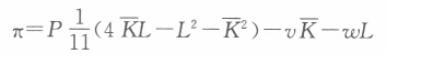
此时,企业所需要的劳动力为
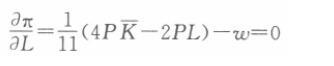

企业利润最大化的一阶条件为:
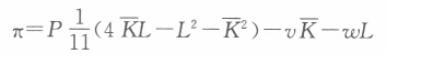
此时,企业所需要的劳动力为
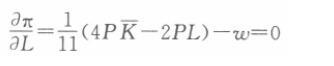
相关考题:
已知某企业的生产函数Q=L2/3K1/3 ,劳动的价格W=2,资本的价格r=1,求:(1)当成本C=3000时,企业实现最大产量时的L、K和Q的值。(2)当产量Q=800时,企业实现最少成本时的L、K和C的值。
已知某企业的成本函数为C=q2+100,C为总成本,q为产量,试问:(1)若产品市场价格p=40,那么产量为多少才可实现最大利润?(2)当产品市场价格达到多少时,该企业才会获得正的市场利润?
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商同质,且在均衡价格上的需求弹性(以绝对值定义)为2,那么均衡时厂商的价格加成率是多少?
已知生产函数为Q =f(K,L)=KL -0. 5L2-0.32K2,Q表示产量,K表示资本,L表示劳动,若K =10,求: (1)写出劳动的平均产量和边际产量函数。 (2)计算当总产量达到极大值时企业雇佣的劳动人数。
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设企业处在长期生产中,w=1,v=4, 企业的最优生产方式是什么?企业的长期成本函数是什么?
一个行业包括一个主导厂商(用z表示)和12个次要厂商(用j表示).主导厂商的总成本函数为Ci=0.0333q3-2q2 +50q,,市场需求曲线为Q=250 -p:主导厂商准确地估计出每个小厂商的成本函数为C.= 2q2+ 1Oq,。主导厂商领导市场价格,并管理自己的产出量,使整个市场供给既不短缺,也无剩余。主导厂商能够正确地预期次要厂商将接受它定的价格。主导厂商的定价是为了使自己的利润最大。 (1)主导厂商的定价为多高?它的产量和利润分别为多少? (2)每个小企业的产量和利润分别为多少?
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设该厂商产品的市场需求函数Q=a-0.5P。若劳动力市场是完全竞争的,求该厂商对劳动的需求函数。
在一个经济体中,产品A与产品B必须联合生产。所有企业使用完全相同的生产技术,每个企业的总成本函数为: C(qA,qB)=1+qA2十qB2 其中,qA和qB分别代表两种产品的产出量。需求方面,消费者们对这两种产品的总需求函数分别为QA(pA)一30 - pA和QB(pB)=40-pB。 其中,pA和pB分别代表两种产品的市场价格。所有企业均为市场价格的“接受者”,且可以自由进出市场。请找出这两个产品的长期均衡价格。
假定一个竞争性厂商,其生产函数为Q=f(L,K)=AL^αK^β,生产要素L和K的价格分别为w和r。 (1)试求在K为不变投入时厂商的短期成本函数。 (2)求厂商的长期成本函数,并讨论不同的规模报酬对平均成本曲线形状的影响。
假定在完全竞争市场中,某企业的生产函数为Q=QK^αL^(1-α) ,产量p=100,a=0.3,资本的租金率R=0.1,企业产品价格P=1 (1)计算最优资本存量。 (2)假设Q预期上升到120,最优资本存量是多少? (3)假定最优资本存量在5年内保持不变,现有的资本存量为100,企业会逐步调整资本存量使其接近于最优值,设A=0.3。第一年的投资量是多少?第二年的资本存量是多少?
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商的生产均面临不变的边际成本1/2,且反需求曲线为p=1-Q,则均衡时两个企业的产量分别是多少?
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时候企业个数
已知某企业的生产函数为Q=,L^(2/3)K^(1/3),劳动的价格,w=2,资本的价格r =1:求 (1)当成本C=3000时,企业实现最大产量时的L、K和Q的均衡值。 (2)当产量Q=800时,企业实现最小成本时的L、K和C的均衡值:
设生产函数为柯布道格拉斯函数Q=L^(1/3)K^(2/3),己知劳动力和资本的价格分别是w=1和r =2, (1)该生产函数代表了哪种类型的规模收益? (2)设企业的生产成本为3000,求两种要素的投入数量与总产量。 (3)设企业的生产产量为800,求两种要素的投入数量与企业所需付出的成本。
考虑柯布一道格拉斯生产函数其中K袁示资本存量,L表示劳动量,要素价格分别是r和w。 (1)求短期成本函数STC(r,w,Y)(短期生产假定资本存量保持不变)。 (2)求长期成本函数LTC(r,w,Y)。 (3)讨论参数a、β的取值与规模报酬之间的关系。
在一个完全竞争的市场,企业使用两种原材料,记为1和2.两种原材料的市场价格均为1每个企业的固定成本为F =32,生产函数为f(x1,x2)=4 x1x2,其中x1是原材料i的使用量。消费者对该产品的需求函数为Q =280 -5p,其中p为市场价格。请找出这个市场的长期均衡价格和企业个数.
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时的单个企业产量和价格
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果均衡价格上的需求价格弹性仍为2,而均衡时行业的HHI指数(即每个企业占有总市场份额的平方和s12+s22)为0.68,以企业市场份额为权重计算的行业平均价格加成率为多少?(价格加成率以勒纳指数(p-MC)/p度量)
已知生产函数为Q= KL -0.5L2-0.32K2;其中,Q表示产量,K表示资本.L表示劳动,令式中K=10,求: (1)写出劳动的平均产量(APPL)函数和边际产量(MPPL)函数。 (2)分别计算当总产量、平均产量和边际产量达到极大值时厂商雇佣的劳动。 (3)求上述条件下厂商总产量、平均产量和边际产量的极大值。
给定CES生产函数Q=(KP+LP)^(1/p),Q为产出,K、L分别为资本和劳动的投入量。 (1)证明该企业规模收益不变。 (2)资本和劳动的边际产量为多少? (3)劳动对资本的边际技术替代率是多少? (4)证明资本和劳动的产出弹性之和等于1。 (5)把这个企业分为两个相同的企业,分立之后的产出之和与原企业的产出有什么变化?详细写出演算过程。
某企业生产一种产品,劳动为唯一可变要素,固定成本既定。短期生产函数Q=-0.1L3+6L22+12L,求: (1)劳动的平均产量函数和边际产量函数。 (2)企业雇用工人的合理范围是多少? (3)若已知劳动的价格为W=480,产品Q的价格为40,则当利润最大时,企业生产多少产品Q?
已知某企业的生产函数为Q=50L^(3/5)K^(3/5)(Q为产量,L为劳动,K为资本),则()A、生产函数为规模报酬递增B、生产函数为规模报酬递减C、生产函数为规模报酬不变D、生产要素报酬递增E、生产要素报酬递减
问答题假定某公司甲的生产函数为:Q=10K0.5L0.5;另一家公司乙的生产函数为:Q=10K0.6L0.4。其中Q为产量,K和L分别为资本和劳动的投入量。 (1)如果两家公司使用同样多的资本和劳动,哪一家公司的产量大? (2)如果资本的投入限于9单位,而劳动的投入没有限制,哪家公司劳动的边际产量更大?
问答题已知某厂商的生产函数为Q=0.5L1/3K2/3;当资本投入量K=50时资本的总价值为500;劳动的价格PL=5。求: (1)劳动的投入函数L=L(Q); (2)总成本函数、平均成本函数和边际成本函数; (3)当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少?
问答题已知企业的生产函数为Q=F(L,K)=LK-0.5L2-0.32K2,Q表示产量,K表示资本,L表示劳动,令K=10。试求劳动的平均产量函数(AP1)和边际产量函数(MP1)。