图示为某闭环系统的信号流图，其中K>0，它的根轨迹为（　　）。A． 整个负实轴B． 整个虚轴C． 虚轴左面平行于虚轴的直线D． 虚轴左面的一个圆

图示为某闭环系统的信号流图，其中K>0，它的根轨迹为（　　）。

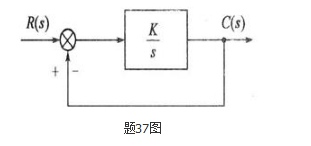
A． 整个负实轴
B． 整个虚轴
C． 虚轴左面平行于虚轴的直线
D． 虚轴左面的一个圆

参考解析

解析：开环传递函数为

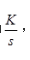
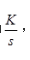
无开环零点且开环极点P1=0。因此，当K从零变到无穷大时，根轨迹为整个负实轴。

相关考题：

一闭环系统的开环传递函数为G(s)=4／(s＋4),则该系统为() A、0型系统，开环放大系数K为4B、I型系统，开环放大系数K为4C、I型系统，开环放大系数K为1D、0型系统，开环放大系数K为1
查看答案
系统的开环传递函数为K／[s(s＋1)(s＋2)],则实轴上的根轨迹为() A、(-2，-1)和(0，∞)B、(-∞，-2)和(-1，0)C、(0，1)和(2，∞)D、(-∞，0)和(1，2)
查看答案
系统闭环根轨迹可以按解析法求出。() 此题为判断题(对，错)。
查看答案
对于以下情况应绘制0°根轨迹的是( ) A 、主反馈口符号为“—” ;B 、除r K 外的其他参数变化时;C 、非单位反馈系统;D 、根轨迹方程(标准形式)为()()1G s H s =+
查看答案
一个单位反馈系统的前向传递函数为K/(s3+5s2+4s)，则该闭环系统的特征方程为s3+5s2+4s+K=0,开环增益为K/4。()
查看答案
根轨迹起点由系统的()决定。A开环极点B开环零点C闭环极点D闭环零点
查看答案
某闭环系统的总传递函数为G（s）=K／（2s3+3s2+K），根据劳斯稳定判据（　　）。A． 不论K为何值，系统不稳定B． 不论K为何值，系统均为稳定C． K>0时，系统稳定D． K
查看答案
某闭环系统的总传递函数为根据劳斯稳定判据判断下列论述哪个是对的？（　　）A． 不论K为何值，系统不稳定B． 当K=0时，系统稳定C． 当K=1时，系统稳定D． 当K=2时，系统稳定
查看答案
对于传递函数的闭环系统，其稳定时K的范围为（　　）。A． 大于0B． 大于0，小于6C． 大于4D． 不等于0
查看答案
如题37图所示的闭环系统（其中K＞0.25）的根轨迹应为（　　）。A． 整个负实轴B． 整个虚轴C． 在虚轴左面平行于虚轴的直线D． 在虚轴左面的一个圆
查看答案
某闭环系统的总传递函数：G（s）=K/2s3 +3s2 +K，根据劳斯稳定判断（）。A.不论K为何值，系统不稳定B.不论K为何值，系统稳定C.K大于0系统稳定D.K小于0系统稳定
查看答案
若某系统的根轨迹有两个起点位于原点，则说明该系统（）。A、含两个理想微分环节B、含两个积分环节C、位置误差系数为0D、速度误差系数为0
查看答案
根轨迹是开环系统某一参数从（）变化到（）时，闭环系统特征方程的根在s平面上变化的（）。
查看答案
绘制根轨迹时，我们通常是从Kg＝0时的闭环极点画起，即开环极点是闭环根轨迹曲线的起点。起点数n就是根轨迹曲线的条数。
查看答案
根轨迹是根据系统开环零极点分布而绘制出的闭环极点运动轨迹。
查看答案
单位负反馈系统的开环传递函数为G（s）=K/（s（0.1s+1）（0.25s+1）），要保证闭环系统稳定，增益K的取值范围为（）。A、K0B、0K14C、K14D、K=14
查看答案
下面有关对根轨迹的描述，说法正确的是（）。A、根轨迹是一种图解方法B、根轨迹避免了求解高阶系统特征方程的困难C、根轨迹可以直观看出系统中某些参数的变化对控制系统闭环特征根分布影响的趋势D、根轨迹在工程上得到了广泛的应用
查看答案
系统的闭环极点与（）、（）和根轨迹增益均有关。
查看答案
以下关于控制系统根轨迹法描述正确的是：（）A、根轨迹法是求解闭环系统特征方程根的一种图式法B、在已知系统开环零、极点在s平面分布的情况下，绘制系统闭环极点在s平面随某一参数变化时的运动轨迹C、绘制根轨迹时，凡是满足幅值条件的点都在根轨迹上D、根轨迹起始于系统开环极点终止于系统开环零点
查看答案
根轨迹是指开环系统某个参数由0变化到∞，（）在s平面上移动的轨迹。A、开环零点B、开环极点C、闭环零点D、闭环极点
查看答案
控制系统频率特性的图示表示方式有：（）A、根轨迹图B、Bode图C、Nyquist图D、信号流图
查看答案
闭环采样系统的极点为Pk.当0k1时该系统瞬态分量收敛。（）
查看答案
在控制系统中，除根轨迹增益K*以外，系统其它参数变化时的根轨迹称为（）。
查看答案
根轨迹是指系统闭环传递函数中某一参数变化时，闭环特征根在根平面上所走过的轨迹。
查看答案
判断题根轨迹是根据系统开环零极点分布而绘制出的闭环极点运动轨迹。A对B错
查看答案
判断题绘制根轨迹时，我们通常是从Kg＝0时的闭环极点画起，即开环极点是闭环根轨迹曲线的起点。起点数n就是根轨迹曲线的条数。A对B错
查看答案
单选题单位负反馈系统的开环传递函数为G（s）=K/（s（0.1s+1）（0.25s+1）），要保证闭环系统稳定，增益K的取值范围为（）。AK0B0K14CK14DK=14
查看答案
热门标签