图示两结构仅竖杆刚度不同，当比例常数n>0时，A、B两截面弯矩绝对值的关系为：A.MA>MB B.MAB C.MA=MB D.不能确定

图示两结构仅竖杆刚度不同，当比例常数n>0时，A、B两截面弯矩绝对值的关系为：

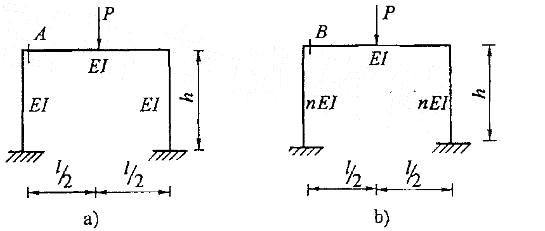
A.MA>MB B.MAB C.MA=MB D.不能确定

参考解析

解析：提示:超静定结构内力与刚度有关，一般来说，刚度大，内力也大。也可用力矩分配的概念分析。

相关考题：

图示结构EI=常数，截面A右侧的弯矩为()A.M/2B.MC.0D.M/(2EI)
查看答案
图示两端铰支压杆的截面为矩形，当其失稳时：
查看答案
图示结构杆长为l，EI=常数，C点两侧截面相对转角φC为：
查看答案
若要保证图示结构在外荷载作用下，梁跨中截面产生负弯矩(上侧受拉) 可釆用：A.增大二力杆刚度且减小横梁刚度B.减小二力杆刚度且增大横梁刚度C. 减小均布荷载D. 该结构为静定结构，与构件刚度无关
查看答案
若要保证图所示结构在外荷载作用下，梁跨中截面产生负弯矩可采用（　　）。 A、增大二力杆刚度且减小横梁刚度 B、减小二力杆刚度且增大横梁刚度 C、减小均布荷载q D、该结构为静定结构，与构件刚度无关
查看答案
图示对称刚架，不计轴向变形，弯矩图为（　　）。A、两杆均内侧受拉B、两杆均外侧受拉C、两杆均部分内侧受拉D、两杆弯矩都为零
查看答案
图示两刚架的EI均为常数，已知EIa=4EIb，则图a)刚架各截面弯矩与图b)刚架各相应截面弯矩的倍数关系为：
查看答案
图示结构EI=常数，A点右侧截面的弯矩为：
查看答案
图示两桁架结构杆AB的内力分别记为N1和N2。则两者关系为： A. N1>N2B. N12C. N1=N2D. N1=-N2
查看答案
在图示结构中，横梁的跨度、刚度和荷载均相同，各加劲杆的刚度和竖杆位置也相同，其中横梁的正弯矩最小或负弯矩最大的是哪个图示的结构？
查看答案
图示梁线刚度为i，长度为ι，当A端发微小转角α，B端发生微小位△ια时，梁两端弯矩（对杆端顺时针为正）为（　　）。
查看答案
图示结构（E为常数），杆端弯矩（顺时针为正）正确的一组为（　　）。
查看答案
若要保证图示结构在外荷载作用下，梁跨中截面产生负弯矩（上侧纤维受拉），可采用（　　）。A、增大二力杆刚度且减小横梁刚度B、减小二力杆刚度且增大横梁刚度C、减小均布荷载qD、该结构为静定结构，与构件刚度无关
查看答案
图示结构，各杆EI=常数，截面C、D两处的弯矩值MC、MD(对杆端顺时针转为正)分别为(单位:kN*m):A. 1. 0,2. 0B. 2. 0,1.0C.-1.0,-2.0D.-2.0,-1.0
查看答案
图示结构当水平支杆产生单位位移时（未注的杆件抗弯刚度为EI），B-B截面的弯矩值为（　　）。
查看答案
图示等截面杆A端的转动刚度系数是：
查看答案
图示两桁架结构杆AB的内力分别记为N1和N2。则两者关系为： A. N1>N2 B. N12 C. N1=N2 D. N1=-N2
查看答案
图示为结构在荷载作用下的M图，各杆EI=常数，则支座B处截面的转角为:
查看答案
图示结构各杆EI=常数，杆端弯矩MDE:
查看答案
在计算钢筋混凝土构件挠度时，根据《混凝土结构设计规范》的建议，可取同号弯矩区段内的哪一项刚度进行计算？( )A.弯矩最大截面的刚度B.弯矩最小截面的刚度C.最大刚度D.平均刚度
查看答案
图示结构中，所有杆件截面特性和材料均相同，跨度和荷载相同，哪种结构a点的弯矩最小？( )A.B.C.D.
查看答案
求图示两跨连续梁的极限荷载。设两跨截面的极限弯矩均为Mu。
查看答案
图示结构A截面弯矩影响线在A处的竖标为l A对B错
查看答案
用力矩分配法计算图示结构，并绘出弯矩图。各杆EI相同且为常数。
查看答案
用力法计算图示结构，并作弯矩图。各杆EI相同且为常数。
查看答案
在计算钢筋混凝土构件挠度时，《混凝土结构设计规范》（GB50010-2002）建议：可取同号弯矩区段内的哪一项刚度进行计算（）A、弯矩最大截面的刚度B、弯矩最小截面的刚度C、最大刚度D、平均刚度
查看答案
长度、横截面积及受轴向外力均相同的钢杆和铝杆，下面说法中正确的是（）。A、两杆的应力分布相同B、两杆的总变形相同C、两杆的抗拉刚度相同D、两杆的应力分布不同
查看答案
热门标签