设函数f(x)在区间[0,1]上具有2阶导数,且,证明: (Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根; (Ⅱ)方程在区间(0,1)内至少存在两个不同实根.
设函数f(x)在区间[0,1]上具有2阶导数,且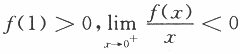 ,证明:
,证明:
(Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根;
(Ⅱ)方程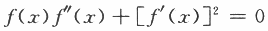 在区间(0,1)内至少存在两个不同实根.
在区间(0,1)内至少存在两个不同实根.
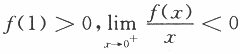 ,证明:
,证明:
(Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根;
(Ⅱ)方程
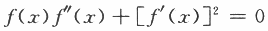 在区间(0,1)内至少存在两个不同实根.
在区间(0,1)内至少存在两个不同实根.参考解析
解析:

相关考题:
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上 A.A当f'(x)≥0时,f(x)≥g(x)B.当f'(x)≥0时,f(x)≤g(x)C.当f"(x)≥0时,f(x)≥g(x)D.当f"(x)≥0时,f(x)≤g(x)
已知函数 (1)求f(x)单调区间与值域; (2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1]。若对于任意x1∈[0,1],总存在x0∈[0,1]使g(x0)=f(x1)成立,求a的取值范围。
问答题设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f″(x)|≤b(其中a、b都是非负常数),c是(0,1)内任一点。 (1)写出f(x)在点x=c处带拉格朗日余项的一阶泰勒公式; (2)证明:|f′(c)|<2a+b/2。
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af″(x)+f(x)=0Bf′(x)+f(x)=0Cf″(x)+f′(x)=0Df″(x)+f′(x)+f(x)=0
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。Af′(x)+f(x)=0Bf′(x)-f(x)=0Cf″(x)+f(x)=0Df″(x)-f(x)=0