随机抽取一个n=100的样本,计算得到x=60,s=15,要检验假设H0:μ=65,H1:μ≠ 65,则检验的统计量的值为()。A.-3.33B.3.33C.-2.36D.2.36
随机抽取一个n=100的样本,计算得到x=60,s=15,要检验假设H0:μ=65,H1:μ≠ 65,则检验的统计量的值为()。
A.-3.33
B.3.33
C.-2.36
D.2.36
B.3.33
C.-2.36
D.2.36
参考解析
解析: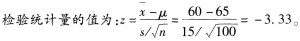
相关考题:
随机区组设计多个样本比较的FriedmanM检验备择假设H0如何写?() A、检验假设H0为多个总体分布位置相同B、备择假设H0为多个总体分布位置不同或不全相同C、检验假设H0为多个样本分布位置相同D、备择假设H0为多个样本分布位置不同或不全相同
在假设检验中,下面的说法正确的是( )。A.建立假设时,有原假设H0和备择假设H1B.已知μ0,可假设H0:μ=μ0,H1:μ≠μ0检验样本均值是否为μ0C.正态总体σ己知时,μ的显著性水平为α的检验采用作为检验统计量D.假设H0:μ≤μ0,H1:μ>μ0,是双侧假设检验E.假设H0:μ=μ0,H1:μ≠μ0,是双侧假设检验
从某个城市中随机抽取15个家庭组成一个随机样本,得到样本均值为84.50元,标准差为14.50元。在μ=0.05的显著性水平下,检验假设H0:μ=90,H1:μ≠90,得到的结论是( )。A.拒绝H0B.不拒绝H0C.可以拒绝也可以接受H0D.可能拒绝也可能接受H0
有关假设检验,下列说法正确的是()A、检验假设针对总体,而不是样本B、进行假设检验时,既可只写出H0或H1,也可同时写出H0和H1C、H0为对立假设D、H0的内容反映了检验的单双侧E、都需先计算出检验统计量后再获得P值
有关假设检验,下列说法正确的是()A、检验假设针对总体,而不是样本B、进行假设检验时,既可只写出HO或H1,也可同时写出H0和H1C、H0为对立假设D、H0的内容反映了检验的单双侧E、都需先计算出检验统计量后再获得P值
设X1,…,X16是取自正态总体N(μ,σ2)的样本,其中μ与σ2均未知.要检验H0:σ=3,则当H0成立时,检验统计量().A、2服从χ2(15)B、服从χ2(15)C、服从χ2(15)D、2服从χ2(16)
单选题检验假设H0:μ≤50,H1:μ>50,随机抽取一个n=16的样本,得到的统计量的值为t=2.5,在α=0.05的显著性水平下,得到的结论是( )。A拒绝H0B接受H0C可以拒绝也可以接受H0D可能拒绝也可能接受H0
单选题设总体X~N(μ1,σ12),Y~N(μ2,σ22),检验假设H0:σ12=σ22;H1:σ12≠σ22;α=0.10,从X中抽取容量为n1=12的样本,从Y中抽取容量为n2=10的样本,算得s12=118.4,s22=31.93,正确的检验方法与结论是( )。A用t检验法,临界值t0.05(17)=2.11,拒绝H0B用F检验法,临界值F0.05(11,9)=3.10,F0.95(11,9)=0.35,拒绝H0C用F检验法,临界值F0.95(11,9)=0.35,F0.05(11,9)=3.10,接受H0D用F检验法,临界值F0.01(11,9)=5.18,F0.99(11,9)=0.21,接受H0
多选题关于x²检验以下说法正确的是 ()Ax²检验的自由度取决于可以自由取值的格子数目Bx²检验的自由度取决于样本含量Cx²值反映了实际频数与理论频数的吻合程度D若检验假设H0成立,则x²值会小E若检验假设h0成立,则x²值会大
单选题有关假设检验,下列说法正确的是()A检验假设针对总体,而不是样本B进行假设检验时,既可只写出H0或H1,也可同时写出H0和H1CH0为对立假设DH0的内容反映了检验的单双侧E都需先计算出检验统计量后再获得P值
单选题已知X1,X2,…,Xn是从某正态总体随机抽取的一个样本,在μ未知的情况下,对于假设的检验问题H0:σ2=σ20,H1:σ2≠σ20,则给定α下,该检验的拒绝域为( )。Aχ2>χ21-α(n-1)Bχ2<χ2α(n-1)Cχ2>χ21-α/2(n-1)Dχ2<χ21-α/2(n-1)
单选题有关假设检验,下列说法正确的是()A检验假设针对总体,而不是样本B进行假设检验时,既可只写出HO或H1,也可同时写出H0和H1CH0为对立假设DH0的内容反映了检验的单双侧E都需先计算出检验统计量后再获得P值
单选题设X1,…,X16是取自正态总体N(μ,σ2)的样本,其中μ与σ2均未知.要检验H0:σ=3,则当H0成立时,检验统计量().A2服从χ2(15)B服从χ2(15)C服从χ2(15)D2服从χ2(16)