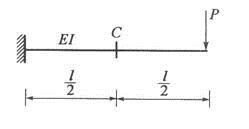
图所示梁C点竖向位移为( )。
图所示梁C点竖向位移为( )。
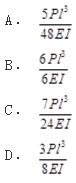

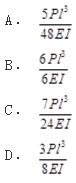
参考解析
解析:采用图乘法计算,在C点加一单位力,做出实际状态下和虚拟状态下的弯矩图,如图,进行图乘可得:
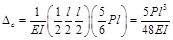
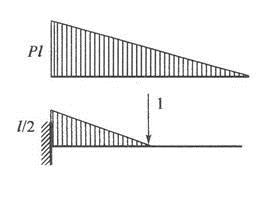
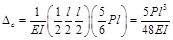

相关考题:
悬臂梁的自由端作用横向力P,若各梁的横截面分别如图a)~h)所示,该力P的作用线为各图中的虚线,则梁发生平面弯曲的是:A.图a)、图g)所示截面梁B.图c)、图e)所示截面梁C.图b)、图d)所示截面D.图f)、图h)所示截面
等截面刚架,矩形截面高h=a/10,材料的线膨胀系数为α,在图所示温度变化下,C点的竖向位移ΔVC之值为( )。 A、80.5aα(↑) B、60aα(↓) C、68aα(↑) D、72aα(↓)
为建立双肢墙连梁未知竖向剪力q(x)的微分方程,需要分析连梁跨中切口处的竖向变形协调条件,切口处的竖向相对位移由三部分组成,其中不包括()A、连梁的轴向变形产生的竖向相对位移B、墙肢弯曲变形产生的竖向相对位移C、墙肢的轴向变形产生的竖向相对位移D、连梁的弯曲变形和剪切变形产生的竖向相对位移
单选题为建立双肢墙连梁未知竖向剪力q(x)的微分方程,需要分析连梁跨中切口处的竖向变形协调条件,切口处的竖向相对位移由三部分组成,其中不包括()A连梁的轴向变形产生的竖向相对位移B墙肢弯曲变形产生的竖向相对位移C墙肢的轴向变形产生的竖向相对位移D连梁的弯曲变形和剪切变形产生的竖向相对位移
单选题已知图5-55(a)所示梁中点c的挠度为 ,则图5-55(b)所示梁c点挠度为()。A AB BC CD D