图示结构EI=常数,截面A右侧的弯矩为()A.M/2B.MC.0D.M/(2EI)
图示结构两杆长均为d,EI=常数。则A点的水平位移为()A.(←)pd³/2B.Pd3/3EI(→)C.Pd3/3EI(←)D.Pd3/6EI(→)
图示结构两杆长均为d,EI=常数。则A点的垂直位移为()A.qd3/2EI(↑)B.qd3/3EI(↓)C.qd4/4EI(↓)D.qd4/6EI(↓)
图示为梁在实际状态下的MP图,EI=常数,则K截面的角位移46.6/EI。()此题为判断题(对,错)。
如图所示,结构外侧温度未变,里侧升高了10℃。已知:矩形截面的高度为h,线膨胀系数为α,则C的水平向位移为( )。
图所示结构各杆温度均升高t℃,且已知EI和EA均为常数,线膨胀系数为α,则点D的竖向位移△Dn为( )。 A、-αta B、αta C、0 D、2αta
图示结构杆长为l,EI=常数,C点两侧截面相对转角φC为:
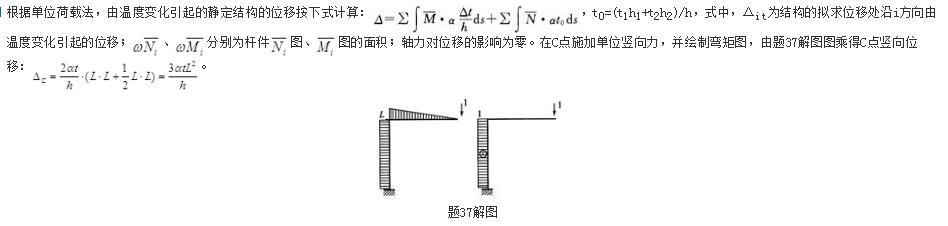
图示结构,EI=常数,截面高h=常数,线膨胀系数为a,外侧环境温度降低t°C,内测环境温度升高t°C,引起的C点竖向位移大小为:
图示刚架材料的线膨胀系数为α,各杆截面均为矩形,截面高度为h,由于图示温度变化引起C点的竖向位移为( )。
已知图示结构EI=常数,A、B两点的相对水平线位移为:
图示结构EI为常数,用力矩分配法计算时,分配系数μBA为( )。
等截面刚架,矩形截面高h=a/10,材料的线膨胀系数为α,在图所示温度变化下,C点的竖向位移ΔVC之值为( )。 A、80.5aα(↑) B、60aα(↓) C、68aα(↑) D、72aα(↓)
图示刚架EI=常数,截面C和D的相对转角为( )。
如图所示的结构(EI=常数)中,D点水平位移(向右为正)为( )。
如图所示组合结构,梁式杆件EI=常数,桁架杆件EA=常数,C点竖向位移为( )。 A、向上 B、向下 C、为零 D、需计算确定
图所示结构,EI=常数,截面高h=常数,线膨胀系数为α,外侧环境温度降低t℃,内侧环境温度升高t℃,引起的C点竖向位移大小为( )。
图示结构,EI为常数。结点B处弹性支撑刚度系数k=3EI/L3,C点的竖向位移为( )。
图示结构,EI=常数,已知结点C的水平线位移为ΔCH=7ql4/184EI(→) 点C的角位移φC应为:
图示结构EI=常数,用力矩分配法计算时,分配系数μA4为:
图示结构EI=常数,A点的竖向位移(向下为正)为( )。{图}A.20Pl3/(3EI)B.16Pl3/(3EI)C.-8Pl3/(3EI)D.8Pl3/(3EI)
图示为结构在荷载作用下的M图,各杆EI=常数,则支座B处截面的转角为:
图示结构,EA=常数,线膨胀系数为。若温度降低t℃.则两个铰支座A、B的水平支座反力的大小为( )。
图示结构各杆EI=常数,其C端的水平位移(→)为: