利用直线趋势法对某类商品住宅2004～2013年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且ΣX＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为（　　）元/㎡。A．5447B．5832C．6987D．7757

利用直线趋势法对某类商品住宅2004～2013年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且ΣX＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为（　　）元/㎡。

A．5447
B．5832
C．6987
D．7757

参考解析

解析：由题意，由于
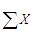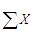=0，所以取2008年对应的X=-1，2009年对应的X=1，则2014年对应的X=6；该方程预测该类商品住宅2014年的平均价格Y=3522+385X=3522+385×6=5832（元/m2）。

相关考题：

对某一时间序列拟合的直线趋势方程为Y=a＋bt,如果该数列中没有趋势,则b的值应该() A.接近1B.小于1C.接近0D.小于0
查看答案
过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1
查看答案
直线z的方程为x-y-2=0，它关于点(1，-4)的对称直线方程为A．x+y-8=0B．x-y-8=0C．z+y+8=0D．x-y+8=0
查看答案
用最小二乘法拟合时间序列的直线趋势方程Y=a＋bt时,若0≤b≤1则该时间 序列的趋势为逐步上升的趋() 此题为判断题(对，错)。
查看答案
斜率为2,且过点(－3,5)的直线方程为() A、y-2x-1=0B、y-2x=7=0C、2y-x-1=0D、y-2x-11=0
查看答案
设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面：A.平行B.垂直C.重合D.相交但不垂直
查看答案
设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。A.B.C.D.
查看答案
设方程y-4y+3y=0的某一积分曲线，它在点(0，2)处与直线x-y+2=0相切，则该积分曲线的方程是( ).A.B.C.D.
查看答案
设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：A.重合 B.平行不重合C.垂直相交 D.相交不垂直
查看答案
某城市某类房地产1998~2006年的价格见表2—24。试利用最小二乘法拟合一直线趋势方程，并用该方程预测该类房地产2007年和2008年的价格。因此，描述该类房地产价格变动长期趋势线的方程为：Y =a+6X=3 522. 22 + 528. 33X 根据该方程计算的1998~2006年该类房地产价格的趋势值。预测该类房地产2007年的价格为：Y =3 522. 22 + 528. 33X=(3 522. 22 + 528. 33X6)元/m2 =6 692. 2 元/m2 预测该类房地产2008年的价格为：Y =3 522. 22 + 528. 33X=(3 522. 22 + 528. 33X7)元/m2=7 220. 53 元/m 2
查看答案
过点(0，1)且与直线x+y+1=0垂直的直线方程为()A.y=xB.y=2x+1C.y=x+1D.y=x-1
查看答案
利用直线趋势法预测某房地产价格，该城市该类房地产2009年～2019年的价格经过方程拟合得到直线趋势方程Y＝6000＋50X，其中Y为商品住宅价格，X为时间，∑X＝0。经验证，该方程拟合度较高，则利用该方程预测该类商品住宅2020年的平均价格为（ ）元/m2。A.6050B.6300C.6550D.6800
查看答案
利用直线趋势法对某类商品住宅2004～2013年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且∑X＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为（　）元/m2。　　A.5447　　B.5832　　C.6987　　D.7757
查看答案
利用直线趋势法对某类商品住宅2010～2019年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且∑X＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2020年的平均价格为（ ）元/m2。A.5447B.5832C.6987D.7757
查看答案
以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ）
查看答案
一圆与Y轴相切，圆心在x一3y=0上，且在直线y=x上截得的弦长为．求圆的方程。
查看答案
设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。A.重合 B.平行不重合 C.垂直相交 D.相交不垂直
查看答案
已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。
查看答案
对某地区1986~1990年商品零售额资料，以数列中项为原点，配合的直线趋势方程Y=610+73X，试利用这个方程预测1992年零售额规模为（）。A、683万B、756万C、829万D、902万
查看答案
设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。A、重合B、平行不重合C、垂直相交D、相交不垂直
查看答案
单选题利用直线趋势法对某类商品住宅2005 ~2013年的平均价格进行分析，拟合成一直线趋势方程y= 3522 +385X，其中y为商品住宅价格，X为时间，且Σx=0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为( ) 元/m2。(2014年试题)A5447B5832C6987D7757
查看答案
填空题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。
查看答案
单选题设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]A重合B平行不重合C垂直相交D相交不垂直
查看答案
单选题过点（1，2）且与直线2x＋y－3＝0平行的直线方程为（　　）．A2x＋y－5＝0B2y－x－3＝0C2x＋y－4＝0D2x－y＝0
查看答案
单选题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。Ay＝exsin2xBy＝－exsin2xCy＝exsinxDy＝－exsinx
查看答案
单选题设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）A重合B平行不重合C垂直相交D相交不垂直
查看答案
单选题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。Ay＝excos2xBy＝－excos2xCy＝exsin2xDy＝－exsin2x
查看答案
热门标签