过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。

过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。

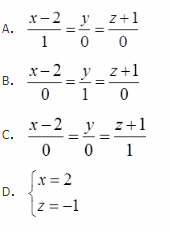
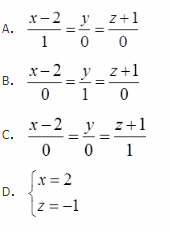
参考解析

解析：垂直于xOy面的直线的方向向量为（0，0，1），由于过点（2，0，－1），则直线的点向式方程为：（x－2）/0＝y/0＝（z＋1）/1。

相关考题：

过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1
查看答案
过原点且垂直于y轴的平面方程为__________
查看答案
在空间直角坐标系中，方程x=2表示( ).A.x轴上的点(2，0，0)B.xOy平面上的直线x=2C.过点(2，0，0)且平行于yOz面的平面D.过点(2，0，0)的任意平面
查看答案
已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。A.B.C.D.
查看答案
球面x2+y2+z2=9与平面x+z=1的交线在xOy坐标面上投影的方程是：
查看答案
过点（1，－2，3）且平行于z轴的直线的对称式方程是（　　）。
查看答案
过点M0(-1，1)且与曲线2ex-2cosy-1 = 0上点(0，π/3)的切线相垂直的直线方程是：
查看答案
已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。
查看答案
过点M(3，-2，1)且与直线L :平行的直线方程是：
查看答案
过点M(3，-2，1)且与平行的直线方程是：
查看答案
过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。
查看答案
过点(0，1)且与直线x+y+1=0垂直的直线方程为()A.y=xB.y=2x+1C.y=x+1D.y=x-1
查看答案
过点P(2，3)且在两条坐标轴上截距相等的直线方程是( )
查看答案
过(1，2)点且平行于向量a=(2，2)的直线方程为＿＿＿＿＿．
查看答案
已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：
查看答案
在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。 (1)求。的值及直线Z的直角坐标方程； (2)圆C的参数方程为试判断直线Z与圆C的位置关系。
查看答案
试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线平行的平面方程。
查看答案
空间曲线在xOy平面的投影方程是（）。
查看答案
设L为从点A（0，-2）到点B（2，0）的有向直线段，则对坐标的曲线积分等于（　　）。A.1B.-1C.3D.-3
查看答案
已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。
查看答案
过原点(0，0，0)且垂直于向量(1，1，1)的平面方程为——．
查看答案
已知中心在坐标原点0的椭圆C经过点A(2，3)且点F(2，0)为其右焦点。 (1)求椭圆C的方程； (2)是否存在平行于OA的直线l，使l与椭圆C有公共点，且直线OA与l的距离等于4，若存在，求l方程；若不存在，请证明。
查看答案
已知圆O的方程为x2+y2=1，过点P(-2，0)作圆的两条切线，切点分别是A，B，则直线AB的方程是( )。
查看答案
在空间直角坐标系中，方程x=2表示（）．A、x轴上的点（2，0，0）B、xOy平面上的直线x=2C、过点（2，0，0）且平行于yOz面的平面D、过点（2，0，0）的任意平面
查看答案
单选题下列判断正确的是（　　）．A垂直于同一条直线的两条直线互相平行B过一点有且只有一条直线和已知直线垂直C过一点有且只有一条直线和一个平面垂直D过平面外一点，有且只有一条直线和已知平面平行
查看答案
单选题在空间直角坐标系中，方程x=2表示（）．Ax轴上的点（2，0，0）BxOy平面上的直线x=2C过点（2，0，0）且平行于yOz面的平面D过点（2，0，0）的任意平面
查看答案
单选题过点（2，1）且与直线y＝0垂直的直线方程为（　　）．Ax＝2Bx＝1Cy＝2Dx＝1
查看答案
问答题求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。
查看答案
热门标签