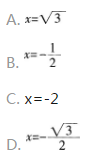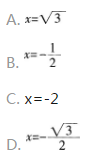已知圆22+y2+4x-8y+11=0,经过点P(1,o)作该圆的切线,切点为Q,则线段PQ的长为 ( )A.10B.4C.16D.8
已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
已知平面π过点(1,1,0)、(0,0,1)、(0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称方程为 ( )。
曲线x2+y2=2x在点(1,1)处的切线方程为.
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。 (1)求证:AB为圆的直径; (2)若AC=BD,AB=5,求弦DE的长。
如右图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙0上,且∠OBA=40°,则∠ADC=_______.
已知圆过A(1,3),B(5,1)两点,且圆心在y轴上,则圆的标准方程为__________。
如图⊙O和⊙O’相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E.证明: (1)AC?BD=AD?AB; (2)AC=AE.
过点(2,0,-1)且垂直于xOy坐标面的直线方程是( )。
已知圆的方程为x2+y2-2x+4y+1=0,则圆上一点到直线3x+4y-10=0的最大距离为( )A.6B.5C.4D.3
过点P(2,3)且在两条坐标轴上截距相等的直线方程是( )
设P是圆x2+y2=2上的一点,该圆在点P的切线平行于直线x+y+2=0,则点P的坐标为
已知圆C,x2+(y-a)2=b若圆C在点(1,2)处的切线与Y轴及点为(0.3)则ab=A.-2B.-1C.0D.1E.2
已知直线l是圆x2+y2=5在点(1,2)处的切线,则l在y轴上的截距为A.2/5B.2/3C.3/2D.5/2E.5
在平面直角坐标系中,以坐标原点0为极点,x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为.直线Z的极坐标方程为且点A在直线Z上。 (1)求。的值及直线Z的直角坐标方程; (2)圆C的参数方程为试判断直线Z与圆C的位置关系。
求过点A(1,-2)的所有直线被圆x2+y2=5截得线段中点的轨迹方程。
椭圆的焦点分别是F1和F2,已知椭圆的离心率.过中心O 作直线与椭圆交于A,B两点,O为原点,若△ABF2的面积是20。 (1)求m的值; (2)直线AB的方程。
已知平面π过点(1,1,0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为( )。
利用直线Line命令结合()捕捉方式可以过已作点作圆的切线或作两个圆的公切线。A、端点B、切点C、交点D、象限点
在同一平面内,直线与圆弧相切,计算切点坐标的方法是()。A、将直线方程与圆方程联立求公共解B、将直线方程代入圆方程求解C、将圆方程代入直线方程求解D、将两个方程相加消元求解
APT自动编程语句中,如下()等方法可以定义圆。A、圆心和半径B、已知不共线三点C、过已知点平行于已知平面D、平面方程E、圆心和切线
单选题AB是平面α的斜线段,A为斜足,若点P在平面α内运动,使得△ABP的面积为定值,则动点P的轨迹是( )。A圆B椭圆C一条直线D两条平行直线
单选题利用直线Line命令结合()捕捉方式可以过已作点作圆的切线或作两个圆的公切线。A端点B切点C交点D象限点
问答题已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
多选题APT自动编程语句中,如下()等方法可以定义圆。A圆心和半径B已知不共线三点C过已知点平行于已知平面D平面方程E圆心和切线
填空题过点P(-1,2)且与圆(x+5)2+(y-5)2=25相切的直线方程为____.
填空题已知点O到直线l上一点P的距离为3cm,圆O的半径为3cm,则直线l与圆的位置关系是____.