过点M(3，-2，1)且与直线L :平行的直线方程是：
过点M(3，-2，1)且与直线L :
平行的直线方程是：
平行的直线方程是：
参考解析
解析：直线L是平面χ - y- z +1 = 0和平面2χ+ y - 3z + 4 = 0的交线，直线L的方向向量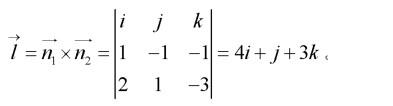
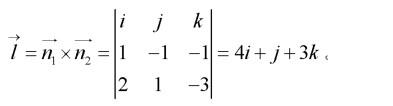
相关考题：
欧几里德几何系统的第五条公理判定：在同一平面上，过直线外一点可以并且只可作一条直线与该直线平行。在数学发展史上，有许多数学家对这条公理是否具有无可争议的真理性表示怀疑和担心。要是数学家的上述怀疑是成立，以下哪项必须成立？（ ）Ⅰ.在同一平面上，过直线外一点可能无法作一条直线与该直线平行。Ⅱ.在同一平面上，过直线外一点作多条直线与该直线平行是可能的。Ⅲ.在同一平面上，如果过直线外一点不可能作多条直线与该直线平行，那么，也可能无法只作一条直线与该直线平行。A.只有ⅠB.只有ⅡC.只有ⅢD.只有Ⅰ和Ⅱ
a、b是两条异面直线，下列结论正确的是（ ）A、过不在a、b上的任一点，可作一个平面与a、b都平行B、过不在a、b上的任一点，可作一条直线与a、b都相交C、过不在a、b上的任一点，可作一条直线与a、b都平行D、过a可以且只可以作一个平面与b平行
已知中心在坐标原点0的椭圆C经过点A(2，3)且点F(2，0)为其右焦点。 (1)求椭圆C的方程； (2)是否存在平行于OA的直线l，使l与椭圆C有公共点，且直线OA与l的距离等于4，若存在，求l方程；若不存在，请证明。
问答题求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。