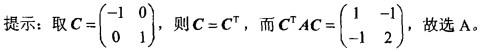设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ). A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同
设A,B为,N阶实对称矩阵,则A与B合同的充分必要条件是().A.r(A)=r（B）B.｜A｜=｜B｜C.A～BD.A,B与同一个实对称矩阵合同
设A,B为正定矩阵,C是可逆矩阵,下列矩阵不是正定矩阵的是().
设A,B都是N阶矩阵,且存在可逆矩阵P,使得AP=B,则().A.A,B合同B.A,B相似C.方程组AX=0与BX=0同解D.r(A)=r(B)
设N阶矩阵A与对角矩阵合同,则A是().A.可逆矩阵B.实对称矩阵C.正定矩阵D.正交矩阵
设矩阵，，则A与B（ ）A.合同，且相似B.合同，但不相似C.不合同，但相似D.既不合同也不相似
设A,B是可逆矩阵，且A与B相似，则下列结论错误的是
设A是实对称矩阵，C是实可逆矩阵，.则（ ）.A.A与B相似B.A与B不等价C.A与B有相同的特征值D.A与B合同
设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同B.矩阵A的特征值都是实数C.存在可逆矩阵P,使P^-1AP为对角阵D.存在正交阵Q,使Q^TAQ为对角阵
设A是三阶矩阵，已知 ，B与A相似，则B的相似对角形为
设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A、等价B、相似C、合同D、正交
单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A等价B相似C合同D正交
单选题设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则（ ）。Ar＞r1Br＜rlCr＝rlDr与r1的关系依C而定
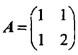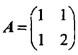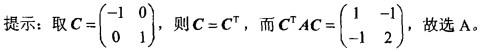
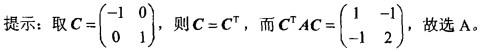
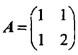,与A合同的矩阵是（ ）。
