设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ). A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同
把复数域C看成实数域R上的线性空间，它的维数是().A.0B. 1C. 2D.无法确定
实数域上的不可约多项式的次数是________次的。
设A,B为,N阶实对称矩阵,则A与B合同的充分必要条件是().A.r(A)=r（B）B.｜A｜=｜B｜C.A～BD.A,B与同一个实对称矩阵合同
设N阶矩阵A与对角矩阵合同,则A是().A.可逆矩阵B.实对称矩阵C.正定矩阵D.正交矩阵
设A是实对称矩阵，C是实可逆矩阵，.则（ ）.A.A与B相似B.A与B不等价C.A与B有相同的特征值D.A与B合同
设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同B.矩阵A的特征值都是实数C.存在可逆矩阵P,使P^-1AP为对角阵D.存在正交阵Q,使Q^TAQ为对角阵
设矩阵(a,b,c,d均为实数)（1）计算；（2）利用（1）的结果，求detM.
设X～N（μ,σ^2）,其分布函数为F(x),对任意实数a,讨论F(-a)+F(a)与1的大小关系.
设A是3阶实对称矩阵,满足，并且r(A)=2. (1) 求A的特征值. (2)当实数k满足什么条件时A+kE正定?
设M为3×3实数矩阵，a为M的实特征值λ的特征向量，则下列叙述正确的是( )。A、当λ≠0时，Ma垂直于aB、当λ＞0时，Ma与a方向相反C、当λ＜0时，Ma与a方向相反D、向量Ma与a共线
实数域上不可约多项式的类型有_________ 种。
设P是3x3矩阵，其秩为2，考虑方程组(1)设的两个解C1、C2为实数，证明也是PX=0的解；(4分) (2)方程组PX=0的解空间的维数是多少 (无需证明)(3分)
设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A、等价B、相似C、合同D、正交
次数大于0的多项式在哪个数域上一定有根？（）A、复数域B、实数域C、有理数域D、不存在
实轴上的某一区域，若其右边开环实数零、极点个数之和为（），则该区域必是根轨迹。
最下的数域是什么？（）A、有理数域B、实数域C、整数域D、复数域
单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A等价B相似C合同D正交
单选题最下的数域是什么？（）A有理数域B实数域C整数域D复数域
单选题次数大于0的多项式在哪个数域上一定有根？（）A复数域B实数域C有理数域D不存在
判断题实数域上的不可约多项式只有一次多项式。A对B错
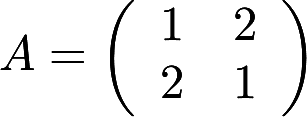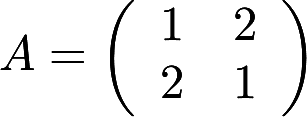，则在实数域上与A合同的矩阵为（ ）
